Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 56

No circuito da Figura 8.102 , determine i ( t ) para t > 0 .

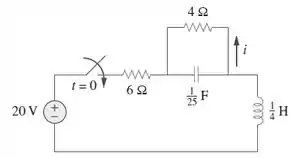
Passo 1

Galerinha, para t < 0 , nós temos um circuito RC sem fontes de alimentação. Assim, i (0) = 0 e v (0) = 0 .

Quando t > 0 , o circuito se torna o seguinte:

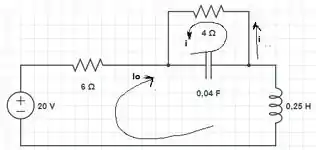
Após ter desenhado o caminho das correntes nas duas malhas do circuito, vamos aplicar a lei das malhas na maior delas:

- 20 + 6 i_0 + 0,25 (d i_0)/(d t) + 25 int (i_0 + i) d t = 0

Se derivarmos essa expressão em relação a t , teremos:

6 (d i_0)/(d t) + 0,25 (d^2 i_0)/(d t^2) + 25 (i_0 + i) = 0

Passo 2

Para a menor malha, temos a seguinte equação:

4 i + 25 int (i + i_0) d t = 0 o u int (i + i_0) d t = - 0,16 i

Derivando a expressão:

4 (d i)/(d t) + 25 (i + i_0) = 0 o u i_0 = - 0,16 (d i)/(d t) - i

(d i_0)/(d t) = - 0,16 (d^2 i)/(d t^2) - (d i)/(d t)

Se substituirmos as últimas expressões encontradas na equação da maior malha,

- 20 - 0,96 (d i)/(d t) - 6 i - 0,05 (d^2 i)/(d t^2) - 0,25 (d i)/(d t) - 4 i = 0

(d^2 i)/(d t^2) + 30,25 (d i)/(d t) + 250 i = - 500

Substituindo (d i)/(d t) por s , temos:

s^2 + 30,25 s + 250 = 0

s_1,2 = (- 30,25 +- sqrt((30,25)^2 - 1000))/(2) = - 15,125 +- j 4,608

Baseado na solução da equação homogênea, temos a seguinte solução para a equação diferencial:

i (t) = I_s + e^(- 15,125 t) (A_1 cos (4,608 t) + A_2 sin (4,608 t)) A

Passo 3

Em t = 0 , temos que i_0 (0) = 0 e i (0) = 0 = I_S + A_1 ou A_1 = - I_s . Conforme t se aproxima do infinito,

i_0 (oo) = (20)/(6 + 4) = 2 A = - i ( oo )

I_s = - i_0 (oo) = - 2 A

A_1 = 2

Derivando a equação da corrente, temos:

(d i)/(d t) = 0 - 15,125 e^(- 15,125 t) (A_1 cos (4,608 t) + A_2 sin (4,608 t)) + e^(- 15,125 t) (- A_1 4,608 sin (4,608 t) + A_2 4,608 cos (4,608 t))

Em t = 0 , (d i (0))/(d t) = 0 . Portanto,

- 15,125 A_1 + 4,608 A_2 = - 30,25 + 4,608 A_2

A_2 = (30,25)/(4,608) = 6,565

E isso nos leva a nossa resposta final

i (t) = { - 2 + e^(- 15,125 t) (2 cos (4,608 t) + 6,565 sin (4,608 t)) A

Resposta

A corrente é igual a:

i (t) = { - 2 + e^(- 15,125 t) (2 cos (4,608 t) + 6,565 sin (4,608 t)) A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura 8.124 mostra um circuito típico de oscilador com diodo túnel. O modelo para o diodo é um resistor não linear com i D = f ( v D ) , ou seja, a corrente no diodo é uma função não linear da tens
Para o circuito da Figura 8.62, determine:(a) i ( 0 + ) e v ( 0 + ) (b) d i ( 0 + ) / d t e d v ( 0 + ) / d t (c) i ( ∞ ) e v ( ∞ )
Para os valores de i 2 0 + , d i 2 0 + d t e v g dados no Ex. 9.1.2, mostre que i 2 no Ex. 9.1.1 é dado por i 2 = - 4 e - t + 7 e - 2 t - e - 6 t A (Sugestão: Substitua a resposta na equação diferenci
Assuma v g = 14 e - 2 tV , i 1 0 + = 6 A e i 2 0 + = 2 A no Ex. 9.1.1, e calcule d i 2 ( 0 + ) / d t (o valor de d i 2 / d t em t = 0 + ).
Calcule a equação que satisfaz a corrente de malha i 2