Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.Problemas - Ex. 15

Se i 1 0 - = 15 / 4 A . Calcule i 1 , i 2 , i c e v c em t = 0 + .

Passo 1

Iae, meus queridos! Td certinho?

Essa questão parece difícil? Te adianto que é bem tranquilinha.

A questão nos deu i 1 0 - = 15 / 4 A , isso significa que o capacitor está carregado. Podemos confirmar essa afirmação fazendo a resistência equivalente do circuito, ignorando o capacitor, e aplicando a Lei de Ohm para achar o “ i e q ”.

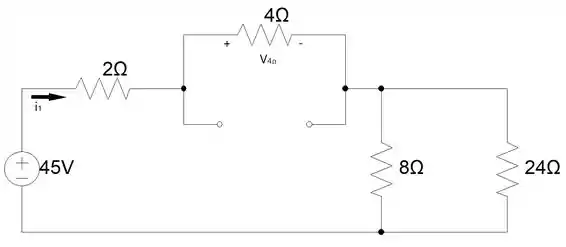
Dessa forma podemos calcular v c em t = 0 - , que obrigatoriamente tem que ser o mesmo valor em t = 0 + . v c 0 - vai ser a mesma tensão no resistor de 4 Ω , portanto.

  v 4 Ω 0 - = v c 0 - =   v c 0 + = 4 · 15 4

v c 0 + = 15 V .

Vamos juntar as informações que podemos adquirir do circuito:

Como a tensão se mantem no instante t = 0 + , podemos afirmar que a corrente no resistor paralelo ao capacitor também se mantém.

i 1 0 + - i c 0 + = 15 4 A .

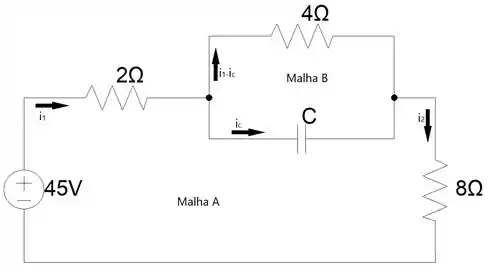
Podemos afirmar também que i 1 0 + = i 2 0 + .

Aplicando analise de malhas na Malha A, podemos tirar a seguinte equação:

2   i 1 + 8   i 2 = 45 - 15

10   i 1,2 = 30

i 1 0 + = i 2 0 + = 3 A .

Pronto, se i 1 0 + - i c 0 + = 15 4 A e i 1 0 + = 3 A , substituímos i 1 0 + na primeira equação.

3 - i c 0 + = 15 4

- i c 0 + = - 3 + 15 4

i c 0 + = - 3 4 A .

Rapidinho né? Bora pra próxima!

Resposta

i 1 0 + = 3 A .

i 2 0 + = 3 A .

i c 0 + = - 3 4 A .

v c 0 + = 15 V .

Exercícios de Livros Relacionados

Calcule a capacidade equivalente vista pelos terminais a-b se todas as capacitâncias são em uF.
As capacitâncias mostradas são todas em uF. Calcule a capacidade equivalente vista pelos terminais a-b.
As capacitâncias mostradas são todas em uF. Calcule a capacidade equivalente vista pelos terminais a-b.
Um capacitor de 400p F e outro de 60p F , ambos de cerâmica, são conectados em paralelo. O produto resistência-capacitância para o capacitor de cerâmica é 10 3 Ω ∙ F . Qual é a capacitância equivalent
No circuito da figura 7.17 , se v 1 0 - = 6 Ve4 J de energia são irradiadores pela ação de chaveamento, calcule v 2 0 -