Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 16

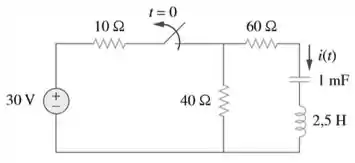
Determine i ( t ) para t > 0 no circuito da Figura 8.70.

Passo 1

Relaxa, galera. Vamo se Ligar e achar a Resposta. Vamos lá! Do circuito, temos que,

Em t = 0 ,

i (0) = 0 , v_c (0) = 40 xx (30)/(50) = 24 V

Para t > 0 , temos um circuito R L C livre de fontes!

alpha = (R)/(2 L) = (40 + 60)/(5) = 20 e omega_0 = (1)/(sqrt(L C)) = (1)/(sqrt(10^(- 3) xx 2.5)) = 20

Passo 2

Sabem o que isso significa? O alpha serem igual ao omega_0 ? O CIRCUITO É CRITICAMENTE AMORTECIDO!

Logo,

i (t) = [(A + B t) e^(- 20 t)] , i (0) = 0 = A

(d i)/(d t) = { [B e^(- 20 t)] + [ - 20 (B t) e^(- 20 t) ] }

Mas,

(d i (0))/(d t) = - ((1)/(L)) [R i (0) + v_C (0)] = - ((1)/(2.5)) [0 + 24]

Portanto,

B = - 9.6 o u i (t) = [- 9.6 t e^(- 20 t)] A

Resposta

i (t) = [- 9.6 t e^(- 20 t)] A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule v para t0 , se o circuito está em regime permanente em t = 0
Encontre o valor máximo para a resposta com amortecimento cúbico do Problema 9.25 e o tempo em que isto ocorre, se i g = 10u - t A
Calcule i , t0 , se não há energia inicial armazenada e:a) C = 1 1 2 F ; b)C = 1 16F ; c) C = 1 32F .
Calcule v para t0 , se a) i_g = 2 u (t) A ; b) i_g = 2 e^(- t) u (t) A .
Sabe-se que a corrente no circuito da Figura P6.35 é io = 2e-5.000t(cos 1.000t + 5 sen 1.000t) Apara t $ 0+. Determine v1(0+) e v2(0+).