Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.4 - Ex. 1

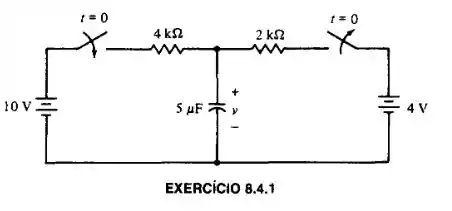
Calcule v para t > 0, se o circuito está em regime permanente em .

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Logo de início, o enunciado já nos fornece uma informação bem importante, o circuito está em regime permanente em , isso já nos indica algumas informações, a primeira é que capacitor, dado ao longo período nesse estado, agora é um circuito aberto, onde obviamente não circula corrente por aquele ponto, e a outra e não menos importante, nós temos nossa “tensão” inicial,

Logo, o circuito em , tem a seguinte configuração:

Podemos transformar essa fonte de tensão de 10 V em uma fonte de corrente (lembra dos conceitos de transformação de fontes independentes?), então, como o resistor está em série com uma fonte de tensão, podemos agora converter em uma fonte de corrente com o resistor em paralelo, logo

Passo 2

Agora, vamos para a parte braçal, as contas, utilizando a equação nodal, nós obtemos o seguinte resultado para a tensão no capacitor

Isolando o termo da derivada, nós temos que

Passando a integral nos dois lados da equação, nós obtemos a seguinte configuração

Essa integral do lado esquerda é igual ao logaritmo neperiano, o famoso , com isso

Em que esse K é uma constante de integração.

Passo 3

Então, não chegamos a uma solução do v já que existe a barreira do logaritmo, como resolver isso? Simples, usa a exponencial para os dois lados com número , com isso

Qual o resultado de ? É o termo dentro do logaritmo, logo, já eliminamos o termo, então temos que

Logo,

Sendo , que vai a constante a ser determinada pelas condições (como em EDO mesmo). Para encontrar A, precisamos da “tensão” inicial quando o regime era permanente, nós já descobrimos isso no inicio do problema, então