Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 10

8.10) Calcule v para t > 0, se o circuito está em regime permanente em t = 0-.

Passo 1

E aí galerinha!! Vamos resolver essa questão juntinhos, beleza??

Nosso circuito é mostrado abaixo:

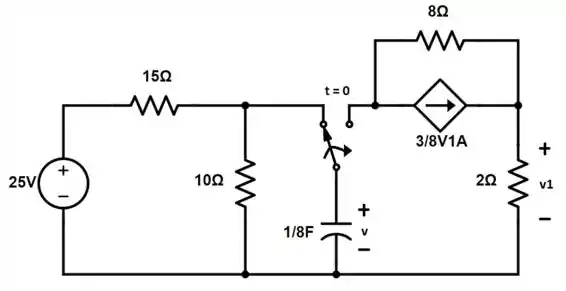
Primeiro, precisamos achar o valor inicial da tensão v antes da chave comutar. Logo, para t

Se trata de um circuito em regime permanente CC, ok? E quando tratamos de circuitos CC o capacitor representa um circuito aberto, lembram disso?? Redesenhando então o circuito vamos achar o valor inicial de v:

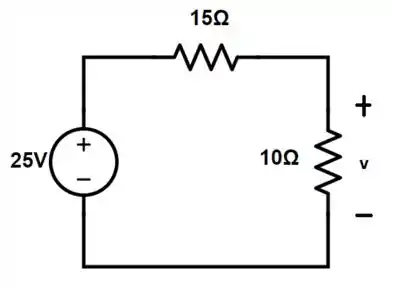
Ficou fácil perceber que a tensão v é a tensão sobre o resistor de 10Ω, né?? Agora é só achar seu valor:

v 0 = 10 10 + 15 * 25 = 10 V

Passo 2

Agora, vamos representar o circuito após a comutação da chave, ou seja, para t > 0:

Definindo os sentidos das correntes e nomeando os nós temos:

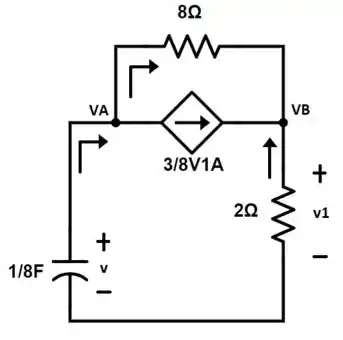
Aplicando LKC nos dois nós:

i C - V B - V A 8 - 3 8 v 1 = 0 ⇒

C d v d t - 1 8 v 1 - v - 3 8 v 1 = 0 ⇒

C d v d t + v 8 - v 1 2 = 0       ( 1 )

v 1 - v 8 + 3 8 v 1 + v 1 2 = 0 ⇒

v 1 = v 8       ( 2 )

Substituindo (2) em (1):

C d v d t + v 8 - v 16 = 0 ⇒ C d v d t + v 16 = 0 ⇒ 1 8 d v d t + v 16 = 0 ⇒ x 8 d v d t + v 2 = 0       ( 3 ) Substituindo d v d t por λ em (3) temos:

λ + 1 2 = 0 ⇒ λ = - 1 2 Como para t > 0, o circuito não apresenta regime permanente, teremos somente a resposta transiente que é dada por:

v t = A e λ t

Basta encontrar o coeficiente A que matamos mais uma questão!! Para encontrá-lo, vamos utilizar a condição inicial para t = 0:

v 0 = 10 = A e - ( 0 2 ) ⇒ A = 10

Por fim, chegamos na equação de v(t):

v t = 10 e - t / 2   V

Prontinhooo, finalizamos essa! Bora pra mais uma??

Resposta

v t = 10 e - t / 2   V

Exercícios de Livros Relacionados

A chave do circuito visto na Figura P7.55 esteve na posição a por um longo tempo. Em t = 0, a chave passa instantaneamente para a posição b. Determine vo (t) e i o (t) para t $ 0+.
A chave do circuito na Figura P7.57 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. No instante em que a chave faz contato com o terminal b, a chave 2 ab
O circuito da Figura P7.56 está em operação por um longo tempo. Em t = 0, a fonte de tensão inverte a polaridade e a fonte de corrente cai de 3 mA para 2 mA. Determine vo (t) para t $ 0.
a) Use os valores dos componentes do Apêndice H para criar um circuito RC de primeira ordem (veja a Figura 7.21) com uma constante de tempo de 250 ms. Use um único capacitor e uma rede de resistores,
A chave do circuito mostrado na Figura P7.22 esteve aberta por um longo tempo antes de seu fechamento em t = 0. Escreva a expressão para a tensão do capacitor, v(t), para t $ 0.