Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 29
Calcule para t>0, se o circuito está em regime permanente em .
Passo 1
Fala, pessoal. Tudo tranquilo? Vocês estão mandando muito nas questões. Mas, vamos continuar praticando. Olha só esse circuito RL, a questão nos pede a corrente no resistor de 4Ω. Vamos fazer juntinhos e arrasar! 💪
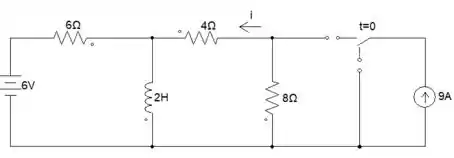
Para essa questão, teremos que fazer a análise em regime permanente e em regime transitório, então vamos começar pelo permanente. Partiu 😎
Vamos ver como fica nosso circuito em regime permanente.
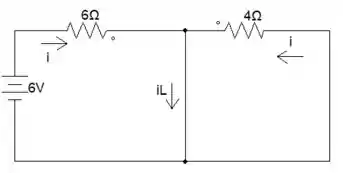
Nessa parte, não teremos corrente passando pelo resistor de 4Ω, pois o indutor se comporta como ideal, então o e para acharmos o , vamos fazer lei de Ohm 😊
Tudo entendido? Fácil essa primeira parte né?
Passo 2
Muito bom! Vamos partir agora para o regime transitório para encontrar nosso . Vamos lá, pessoal! Olha só como vai ficar nosso circuito agora:
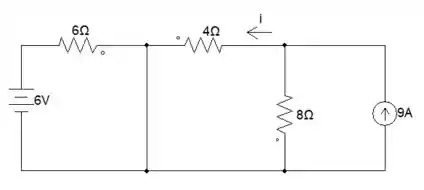
Percebeu que temos uma fonte de corrente em paralelo com um resistor? Nós podemos fazer lei de Ohm neles e transformar a fonte de corrente para uma fonte de tensão!
Show de bolinhas! Olha só como que fica o circuito agora:
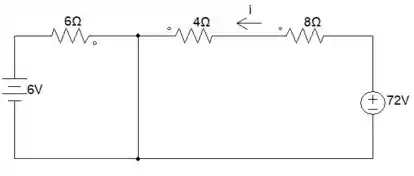
Maravilha, pessoal! Já perceberam que ficamos com duas malhas? Agora, podemos aplicar LKT nas malhas. Vamos definir duas correntes para cada malha, Vamos lá.
Malha 1:
Malha 2:
Vamos formar um sistema de equações:
:
Vamos adotar
Passo 3
Massa! Tá tirando onda.
Se liga! A gente vai ter que descobrir a resposta natural e a resposta forçada dessa EDO. Vamos começar pela resposta natural 😉.
Agora a resposta forçada.
Show de bola🤩. E, para acharmos nosso vamos somar as duas respostas.
Ops! Mas, e a constante A quanto vale? Vamos descobrir juntinhos!
Substituindo na equação teremos:
Passo 4
Estamos quase terminando! Ainda não temos a corrente que está passando do resistor de 4Ω. Vamos descobrir o e substituir na equação da Malha 2. Vamos lá.
Substituindo na equação da Malha 2: