Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 7

Calcule i para t > 0 , se o circuito está em regime permanente em t = 0 - .

Passo 1

Faaaaalaa, galerinha. Tudo bem? Já está craque em circuito RC, que tlgd, mas vamos continuar praticando para ficar melhor ainda!

Olha só esse circuito que massa, dá pra trabalharmos coisas bem importantes. Então, vamos lá! 💪

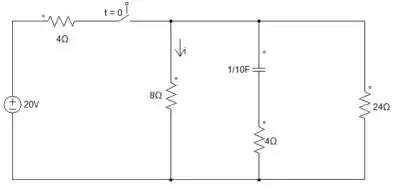
Analisando o circuito, percebemos que vamos precisar fazer a análise de quando o regime for permanente e quando for transitório. Mas, você já sabe o que é cada um? Vamos lembrar aqui bem rapidinho😉.

Regime transitório, é o período que apresenta variação e nós analisamos o instante em que não há mais essa variação ou pouca variação.

Regime permanente, é o período em que não há mais variação ou pouca variação em sua saída.

Refrescou a memória?

Dito isso, vamos começar a analisar esse circuito em regime permanente. Quando está em regime permanente consideramos que o capacitor está aberto, porque não terá corrente nele. Então, nosso circuito fica assim:

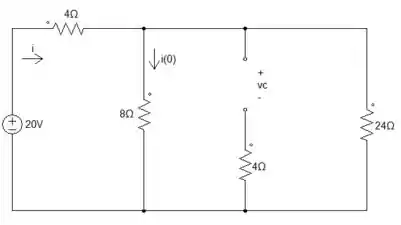
Vamos ter que fazer associação entre os resistores.

Analisando, percebemos que o resistor de 8Ω está em paralelo com o de 24Ω.

R 8 // R 24 = 8 ⋅ 24 8 + 24

R 8 // R 24 = 192 32

R 8 // R 24 = 6 Ω

O resistor de 6 Ω está em série com o de 4 Ω .

R 6   +   R 4   = 6 + 4

R 6   +   R 4   = 10Ω

Assim, fica nosso circuito:

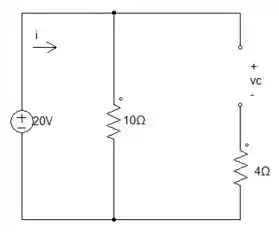
Agora, vamos descobrir nosso i .

V = R ⋅ i

i = 20 10

i = 2 A

Após isso, podemos fazer divisor de tensão e encontrar nosso i 0 .

i 0 = i ⋅ 24 24 + 8

i 0 = 2 ⋅ 24 32

i 0 = 3 2 A

Estamos quase terminando essa parte! Agora, precisamos fazer divisor de tensão para acharmos o nosso v 0 . Vamos lá!

v 0 = v ⋅ 6 4 + 6

v 0 = 20 ⋅ 6 10

v 0 = 12 V

Passo 2

Mandou bem dmsss! Já achamos todos os valores para nosso circuito em regime permanente. Agora, partiu acharmos os resultados dele em regime transitório?!

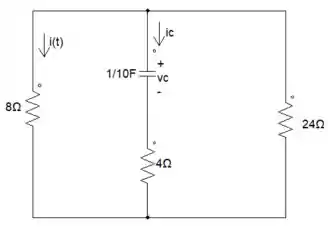
Vamos ter que fazer associação entre os resistores mais uma vez.

O resistor de 8Ω está em paralelo com o de 24Ω.

R 8 // R 24 = 8 ⋅ 24 8 + 24

R 8 // R 24 = 192 32

R 8 // R 24 = 6 Ω

O resistor de 6 Ω está em série com o de 4 Ω .

R 6   +   R 4   = 6 + 4

R 6   +   R 4   = 10Ω

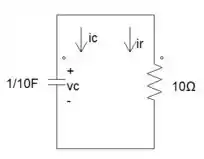
Depois de acharmos nosso circuito equivalente, vamos achar o τ .

τ = R e q ⋅ C

τ = 10 ⋅ 1 10

τ = 1 s

Facinho né?! Feito isso, vamos achar nossa equação v t . Já sabemos que v 0 = 12 V , então nosso A será 12.

v t = 12 e - t 1  

v t = 12 e - t   V

Passo 3

Sensacional! Falta pouquinho agora. Só precisamos achar agora, a equação do i ( t ) . Mas, antes precisamos saber quanto de corrente está passando no capacitor. Para isso, vamos usar uma velha amiga nossa: a lei de Ohm.

i c = v t R

i c = 12 e - t 10

i c =   1,2 e - t A

Agora, sim! Vamos saber quanto vale nosso i ( t ) . Vamos fazer divisão de corrente e tcharaaan!

i t =   i c ⋅ R 24 R 24 + R 8

i t =   1,2 e - t ⋅ 24 24 + 8

i t =   0,9 e - t A .

Resposta

i t =   0,9 e - t A

Exercícios de Livros Relacionados

A chave no circuito da Figura P7.88 esteve fechada por um longo tempo. A tensão máxima nominal do capacitor de 1,6 mF é 14,4 kV. Em quanto tempo, depois da abertura da chave, a tensão no capacitor alc
A forma de onda de tensão mostrada na Figura P7.84 (a) é aplicada ao circuito da Figura P7.84(b). A corrente inicial no capacitor é igual a zero.Calcule v 0 ( t ) .Faça um gráfico de v 0 t em função d
A fonte de tensão no circuito da Figura P7.83(a) está gerando o sinal mostrado na Figura P7.83(b). Não há nenhuma energia armazenada em t=0.Determine as expressões para v 0 ( t ) que sejam válidas par
Calcule v para t0 se não existe energia inicial armazenada.