Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 17

O circuito mostrado está em regime permanente cc em t = 0 .   Calcule v para t>0.

Passo 1

Iae, galerinha. Tudo bem?

Tá praticando muito para tirar aquele 10 na prova? Vamos fazer mais uma questão de circuito RL, só que dessa vez, nosso circuito tem uma fonte dependente. Calma! Não se assustar, vamos fazer juntos e vai dar tudo certo!

Viu nosso circuito? Bonitão né?. Pra começar, vamos analisar o circuito em regime permanente, para isso temos que desconectar o indutor. Se liga como o circuito fica agora:

Show de bola! Agora, ficamos com duas malhas. Analisando o lado da fonte dependente, percebemos que não está passando corrente, então i = 0 . Analisando o outra malha, dá pra acharmos o valor do i L ( 0 ) , para isso vamos fazer a lei de Ohm no resistor de 5Ω.

V = R ⋅ I

I = V R

I = 10 5

I = 2 A

Como i L 0 = I , então i L 0 = 2 A

Passo 2

Tirou onda dmsss! Depois de acharmos nosso i L 0 no regime permanente, vamos partir parar acharmos o nosso v ( t ) do circuito. Partiu fazermos o regime transitório? Dá uma olhadinha como fica o circuito agora:

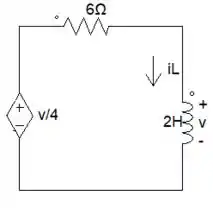
Nessa parte, iremos começar fazendo análise da malha e, assim, acharmos nossa EDO. Vamos lá!

v 4 - 6 i L - v = 0

Como já sabemos, o v = l ⋅ d i d t , então:

l 4 ⋅ d i d t - 6 i L - l ⋅ d i d t = 0

- 3 4 ⋅ l d i d t = 6 i L

Maravilha! Já achamos nossa EDO, vamos descobrir o r agora.

- 3 4 r = 6

r =   6 ⋅ - 4 3

r =   - 8 2

r =   - 4

Passo 3

Vocês são feras! Feito isso, vamos jogar na equação do i t . Mas,peraí, quanto vale nossa constante A? Nosso A vale o mesmo que o i 0 , valor encontrado no passo 1.

i t = A e - R t L  

i t = 2 e - 4 t A  

Passo 4

Show de bola, galera! Estamos quase terminando. Já temos que precisamos para acharmos nosso v ( t ) . Como sabemos, o v = l ⋅ d i d t , então vamos substituir o valor da corrente do indutor na nossa EDO 😉

- 3 4 ⋅ l d i d t = 6 i L

- 3 4 ⋅ l d i d t = 6 ⋅ 2 e - 4 t

l d i d t = 1 2 e - 4 t ⋅   - 4 3

l d i d t = - 1 6 e - 4 t V

Resposta

v t = - 1 6 e - 4 t V

Exercícios de Livros Relacionados

A chave no circuito da Figura P7.46 esteve aberta por um longo tempo, antes de fechar em t = 0. Determine vo (t) para t $ 0+.
A chave no circuito da Figura P7.47 esteve na posição 1 por um longo tempo. Em t = 0, ela passa instantaneamente para a posição 2. Em quantos milissegundos, depois do acionamento da chave, vo atinge 1
A chave liga-antes-interrompe-depois do circuito da Figura P7.49 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. Determine a) vo (t), t $ 0+. b) i 1 (t),
Suponha que a chave no circuito da Figura P7.51 esteve na posição a por um longo tempo e que em t = 0 ela é colocada na posição b. Determine (a) vC(0+); (b) vC(q); (c) t para t . 0; (d) i(0+); (e) vC,
A chave no circuito da Figura P7.14 esteve fechada por um longo tempo antes de abrir em t = 0. Determine vo (t) para t $ 0+.