Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 9.Problemas - Ex. 9

Calcule v para t > 0 , se o circuito está em regime permanente em t = 0

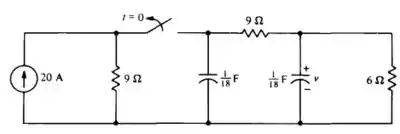
Passo 1

Fala aí pessoal tudo blz?

Nessa questão ele pede para calcular v   para t > 0 , sendo o regime permanente para t = 0

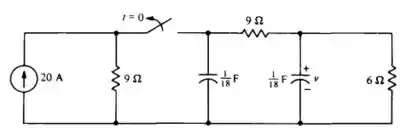
Pode ficar calminho que você vai entender legal, só confia.

Passo 2

Sabendo que,

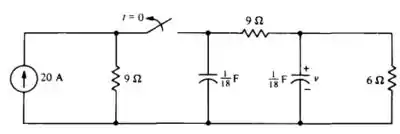
Temos,

No circuito RLC, temos

y t = c 1 . e λ t . cos ⁡ β t + c 2 . e λ t . sin ⁡ β t

y t = 5 4 e - t - 9 e - 6 t   V

Espero ter ajudado, e até a próxima.

Resposta

y t = 54 e - t - 9 e - 6 t   V

Exercícios de Livros Relacionados

Determine a tensão no capacitor de 80n F para o circuito descrito no Problema 8.39. Admita que a polaridade de referência para a tensão no capacitor seja positiva no terminal superior.
Sabe-se que a corrente no circuito da Figura 8.3 é i = B 1 e - 2000 t cos ⁡ 1500 t + B 2 e - 2000 t sin ⁡ 1500 t , t ≥ 0 O capacitor tem um valor de 80n F ; o valor inicial da corrente é de 7,5m A , e
A energia inicial armazenada no capacitor de 31,25n F no circuito da Figura P8.41 é 9μ J . A energia inicial armazenada no indutor é igual a zero. As raízes da equação característica que descreve a re
a) Altere a resistência do circuito que você projetou no Problema 8.43 (a) de modo que a resposta seja subamortecida. Continue a utilizar os componentes do Apêndice H. Calcule as raízes da equação car
a) Projete um circuito R L C em série (veja a Figura 8.3) usando valores de componentes do Apêndice H, com uma frequência angular de ressonância de 20k r a d / s . Escolha um resistor ou crie uma rede