Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 40

Determine a tensão no capacitor de 80   n F para o circuito descrito no Problema 8.39. Admita que a polaridade de referência para a tensão no capacitor seja positiva no terminal superior.

Passo 1

Salve, salve, pessoal! Vamos começar uma questão que faz uso de dados da questão anterior. Sendo assim, vamos repetir as informações que forem úteis aqui. O problema 8.39 faz uso da figura 8.3, então vamos começar exibindo-a:

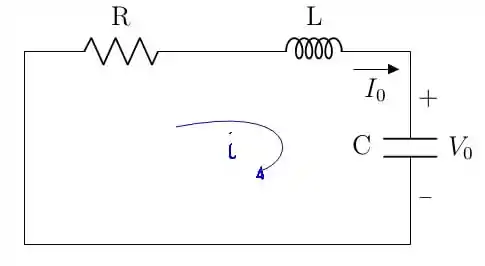
Além disso, foi-nos dado um valor de i ( t ) na forma genérica

i = B 1 e - 2000 t cos ⁡ 1500 t + B 2 e - 2000 t sin ⁡ 1500 t ,     t ≥ 0

Pois bem, vamos mostrar o circuito com os valores obtidos na questão anterior:

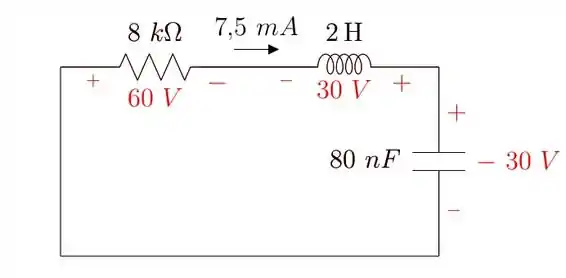
Aqui foi frisado o valor negativo da tensão no capacitor porque ficará mais claro na hora de usarmos seu valor nos cálculos da resolução.

Passo 2

Como a corrente tem uma resposta do tipo subamortecida, a tensão também será assim e genericamente terá a forma

v c t = Z 1 e - α ⋅ t cos ⁡ ω d ⋅ t + Z 2 e - α ⋅ t sin ⁡ ω d ⋅ t

Aí vem a pergunta de milhões: De onde vem essa constante Z ? Bem, respondo! Trata-se de uma constante, então podemos escolher a letra que quisermos. Tá, ok, mas por que a letra “Z”, especificamente, você provavelmente deve estar se perguntando. A resposta é simples! Eu sou muito fã de Dragon Ball Z, por isso, resolvi fazer menção ao desenho nessa questão.

Pois bem, vamos continuar a questão. Usando os valores encontrados na questão anterior, teremos que a tensão no capacitor será

v c t = Z 1 e - 2000 ⋅ t cos ⁡ 1500 t + Z 2 e - 2000 ⋅ t sin ⁡ 1500 t

Passo 3

Vamos começar escolhendo t = 0 para a tensão:

v c 0 = Z 1 e - 2000 ⋅ 0 cos ⁡ 1500 ⋅ 0 + Z 2 e - 2000 ⋅ 0 sin ⁡ 1500 ⋅ 0

Como cos ⁡ 0 = 1 ; sin ⁡ 0 = 0 e e 0 = 1 , temos que

v c 0 = Z 1

Assim,

Z 1 = - 30   V

Passo 4

A corrente no capacitor é dada por

i c t = C ⋅ d v t d t ⇒ d v t d t = i c t C = 0,0075 80 ⋅ 10 - 9 ⇒ d v t d t = 93750

Além disso, vamos derivar a expressão de v c ( t ) :

d v c t d t = Z 1 - 2000 e - 2000 t cos ⁡ 1500 t + e - 2000 t ( - sin ⁡ 1500 t ) 1500 + Z 2 [ - 2000 e - 2000 t sin ⁡ 1500 t + e - 2000 t cos ⁡ 1500 t ( 1500 ) ]

Substituindo o valor de Z 1 e escolhendo t = 0 , obtemos:

d v c 0 d t = 93750 = - 30 ⋅ ( - 2000 ) + 1500 ⋅ Z 2

⇒ 1500 Z 2 = 93750 - 60000

⇒ Z 2 = 33750 1500 ∴ Z 2 = 22,5   V

Assim, a tensão é dada por

v c t = - 30 e - 2000 t cos ⁡ 1500 t + 22,5 e - 2000 t sin ⁡ 1500 t   V ,     t ≥ 0

Pronto, chegamos ao final e já vamos emendar com a próxima questão!

Resposta

v c t = - 30 e - 2000 t cos ⁡ 1500 t + 22,5 e - 2000 t sin ⁡ 1500 t   V ,     t ≥ 0

Exercícios de Livros Relacionados

A resposta natural do circuito na Figura 8.1 é v t = 120 e - 400 t cos ⁡ 300 t + 80 e - 400 t sin ⁡ 300 tV , quando o capacitor é de 250 μ F . Determine (a) L; (b) R; (c) V 0 ; (d) I 0 e (e) i L ( t )
A resistência no Problema 8.1 é reduzida para 100Ω . Determine a expressão para v(t) quando t ≥ 0 .
A resistência, indutância e capacitância de um circuito RLC em paralelo são 2.000 Ω , 250 mH e 10 nF, respectivamente. a) Calcule as raízes da equação característica que descreve a resposta de tensão
Sabe-se que a resposta de tensão para o circuito da Figura 8.1 é v t = D 1 t e - 80 t + D 2 e - 80 t ,t ≥ 0 . A corrente inicial no indutor ( I 0 ) é -25 mA, e a tensão inicial no capacitor ( V 0 ) é
Suponha que o indutor, no circuito mostrado na Figura 8.1, tenha um valor de 10 mH. A resposta de tensão para t ≥ 0 é v t = 40 e - 1000 t - 90 e - 4000 tV . a) Determine os valores numéricos de ω 0 ,