Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 39
Sabe-se que a corrente no circuito da Figura 8.3 é
O capacitor tem um valor de ; o valor inicial da corrente é de , e a tensão inicial no capacitor é . Determine os valores de .
Passo 1
Faaaaaaaaaaaaaaaala, galera! Beleza? Dando início aos exercícios da seção 8.4, vamos facilitar a sua vida e vamos colocar o circuito da figura 8.4 para podermos fazer o que se pede.
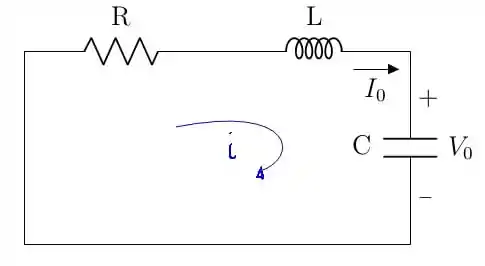
Ok! Estamos diante de um circuito RLC série sem fonte. Também nos é dado a corrente em função do tempo. Assim, vamos começar pelo mais fácil. Vamos retirar da equação os valores de e :
Com essas duas informações, podemos encontrar que será útil no cálculo da indutância:
Vamos deixar esse valor ao quadrado para facilitar as contas abaixo. Sabemos que a equação que relaciona e é:
mas como já temos o valor de , podemos reescrever
Além disso, o valor de pode ser obtido de
Passo 2
Dando continuidade à análise, vamos precisar trabalhar em cima do circuito para encontrar as duas outras constantes. Escolhendo para analisar a corrente, obtemos o seguinte:
Como ; e , temos que
Resta então encontrar a outra constante.
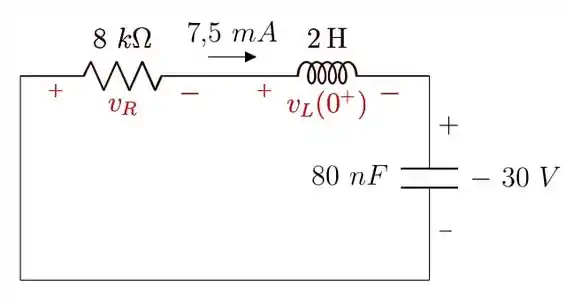
Passo 3
No enunciado nos foi dito a corrente inicial circuito e a tensão no capacitor. Podemos usar a informação da corrente para encontrar a tensão no resistor usando a Lei de Ohm e após isso usar a LKT para encontrar a tensão no indutor. Vamos mostrar isso num desenho
A figura já ajuda a esclarecer um pouco o que foi dito. Perceba que a polaridade da tensão no capacitor é diferente da sugerida na figura. Isso implica numa mudança de polaridade durante a análise:
Assim:
Passo 4
A tensão no indutor é dada por
Assim,
Também podemos obter uma expressão para a partir da equação da corrente fornecida no enunciado. Vamos reescrever a equação da corrente:
Derivando essa expressão, vamos obter:
Substituindo o valor de e escolhendo , obtemos:
E assim, concluímos a primeira de todas as questões dessa seção. Vamos em frente!