Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 41

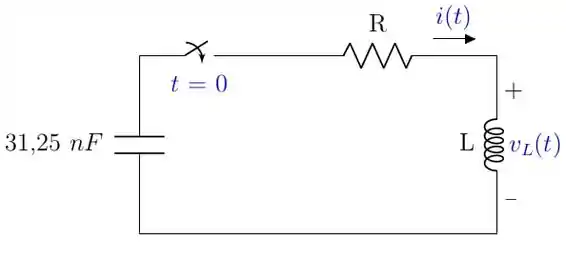
A energia inicial armazenada no capacitor de 31,25   n F no circuito da Figura P8.41 é 9   μ J . A energia inicial armazenada no indutor é igual a zero. As raízes da equação característica que descreve a resposta natural da corrente i são - 4000   s - 1 e - 16000   s - 1 .

a) Determine os valores de R e L .

b) Determine os valores de i ( 0 ) e d i ( 0 ) / d t imediatamente após o fechamento da chave.

c) Determine i ( t ) para t ≥ 0 .

d) Quantos microssegundos depois que a chave é fechada a corrente alcança seu valor máximo?

e) Qual é o valor máximo de i , em miliampères?

f) Determine v L ( t ) para t ≥ 0 .

Passo 1

Show de bola, galera! Vamos resolver essa questão que promete ser trabalhosa, mas vamos ver se ela é tudo isso mesmo.

a)

Vamos começar a questão olhando para o fato de que as raízes da equação característica são reais e distintas, logo, a resposta é superamortecida. Pois bem, a equação 8.57 nos mostra que

s 1,2 = - α ± α 2 - ω 0 2

Para usarmos essa equação, devemos notar que o valor positivo da raiz quadrada deve ser usado com o maior valor de s e o valor negativo da raiz quadrada, o menor valor de s . Assim

- 4000 = - α + α 2 - ω 0 2 ⇒ - 4000 + α = α 2 - ω 0 2

Elevando ambos os membros ao quadrado, obtemos

16.000.000 - 2 ⋅ 4000 ⋅ α + α 2 = α 2 - ω 0 2

8000 ⋅ α - ω 0 2 = 16.000.000

Resolvendo agora para o outro valor de s , obtemos

- 16000 = - α - α 2 - ω 0 2 ⇒ - 16000 - α = - α 2 - ω 0 2

Elevando ambos os membros ao quadrado, obtemos

256.000.000 - 2 ⋅ 16000 ⋅ α + α 2 = α 2 - ω 0 2

32000 ⋅ α - ω 0 2 = 256.000.000

Juntando as duas equações, vamos obter o seguinte sistema

8000 ⋅ α - ω 0 2 = 16.000.000 32000 ⋅ α - ω 0 2 = 256.000.000

Esse sistema pode ser resolvido por adição, ou até mesmo colocado numa calculadora científica. Fazendo isso, vamos obter como resultados

α = 10000 r a d s                   e                 ω 0 2 = 64 ⋅ 10 6

De repente você pode estar se perguntando o motivo de usarmos o valor ao quadrado da frequência, mas isso pode ser verificado agora:

ω 0 = 1 L C ⇒ ω 0 2 = 1 L C ⇒ L = 1 C ω 0 2

⇒ L = 1 31,25 ⋅ 10 - 9 ⋅ 64 ⋅ 10 - 6 ∴ L = 0,5   H

Além disso, sabemos que

α = R 2 L ⇒ R = 2 ⋅ α ⋅ L ⇒ R = 2 ⋅ 0,5 ⋅ 10000 ∴ R = 10000   Ω

Passo 2

b)

Considere o circuito antes da chave fechar. Como não foi dito nada, supomos que ele esteja em regime permanente, o que significa que o capacitor funciona como um circuito aberto. Isso significa que após a chave comutar, a corrente que circula no indutor não poderá variar instantaneamente e como não havia corrente circulando em t = 0 - , não haverá corrente circulando no indutor em t = 0 + , consequentemente não haverá corrente no circuito, logo

i 0 = 0   A

Além disso, foi-nos dada a energia no capacitor cuja relação é

E c a p = C V 2 2

mas como estamos falando de um regime transitório, vamos colocar esta relação como

E c a p = C v c a p 2 0 2 ⇒ v c a p 2 0 = 2 ⋅ E c a p C = 2 ⋅ 9 ⋅ 10 - 6 31,25 ⋅ 10 - 9

⇒ v c a p 2 0 = 576 ⇒ v c a p 0 = 24   V

Agora, podemos usar a tensão no capacitor para achar a relação d i ( 0 ) / d t :

v c t = L ⋅ d i t d t ⇒ d i 0 d t = v c 0 L = 24 0,5 ∴ d i 0 d t = 48 A s

Passo 3

c)

Como já foi discutido no Passo 1, a resposta é superamortecida, logo, sua forma é do tipo

i t = A 1 e - 4000 t + A 2 e - 16000 t

Escolhendo t = 0 , vamos obter

i 0 = A 1 e - 4000 ⋅ 0 + A 2 e - 16000 ⋅ 0 ⇒ A 1 + A 2 = 0

Derivando a expressão da corrente, obtemos

d i t d t = A 1 - 4000 e - 4000 t + A 2 - 16000 e - 16000 t

Escolhendo t = 0 , vamos obter

d i 0 d t = A 1 - 4000 e - 4000 ⋅ 0 + A 2 - 16000 e - 16000 ⋅ 0

⇒ - 4000 A 1 - 16000 A 2 = 48

Assim, o sistema que teremos que resolver será

A 1 + A 2 = 0 - 4000 A 1 - 16000 A 2 = 48

Esse sistema vai nos dar as seguintes soluções:

A 1 = 0,004   A                           e                               A 2 = - 0,004   A

Logo, a corrente será dada por

i t = 0,004 e - 4000 t - 0,004 e - 16000 t   A ,     t > 0

Passo 4

d)

Quando queremos estudar o máximo ou o mínimo de uma função, temos que estudar a derivada dela. Isso é uma das primeiras coisas que aprendemos lá em Cálculo 1. Sendo assim, temos que se

i t = 0,004 e - 4000 t - 0,004 e - 16000 t   A

então

d i t d t = 0,004 - 4000 e - 4000 t - 0,04 - 16000 e - 16000 t

⇒ d i t d t = - 16 e - 4000 t + 64 e - 16000 t

Quando a derivada vale zero, a corrente atinge seu valor máximo. Assim

d i d t = 0 ⇒ - 16 e - 4000 t + 64 e - 16000 t = 0

⇒ = 16 e - 4000 t = 64 e - 16000 t ⇒ e - 4000 t e - 16000 t = 64 16 ⇒ e 12000 t = 4

Para sairmos deste ponto, teremos que usar logaritmos:

ln ⁡ e 12000 t = ln ⁡ 4 ⇒ 12000 t = ln ⁡ 4 ⇒ t = ln ⁡ 4 12000

∴ t = 115,5   μ s

Passo 5

e)

Esse item é bastante simples porque basta apenas pegar o tempo encontrado no Passo 5 e aplicar na equação da corrente:

i m a x = i 115,5 ⋅ 10 - 6 = 4 ⋅ e - 4000 × 115,6 ⋅ 10 - 6 - 4 ⋅ e - 16000 × 115,6 ⋅ 10 - 6

∴ i m a x = 1,89   m A

Passo 6

f)

Para encontrarmos v L ( t ) basta aplicarmos a definição de tensão no indutor:

v L t = L ⋅ d i d t

No Passo 4 já encontramos o valor de d i / d t , então

v L t = 0,5 ⋅ - 16 e - 4000 t + 64 e - 16000 t

∴ v L t = - 8 e - 4000 t + 32 e - 16000 t   V ,     t > 0  

Resposta

a)

L = 0,5   H                       e                         R = 10000   Ω

b)

i 0 = 0   A                        e                           d i 0 d t = 48 A s

c)

i t = 0,004 e - 4000 t - 0,004 e - 16000 t   A ,     t > 0

d)

t = 115,5   μ s

e)

i m a x = 1,89   m A

f)

v L t = - 8 e - 4000 t + 32 e - 16000 t   V ,     t > 0

Exercícios de Livros Relacionados

Sabe-se que a resposta natural para o circuito mostrado na Figura 8.1 é v t =- 11 e - 100 t+20 e - 400 tV ,t ≥0 . Se C = 2 μ F e L = 12,5 H, determine i L ( 0 + ) em miliamperes.
A resistência do resistor no circuito do Exemplo 8.4 é alterada para 3.200 Ω . a) Determine a expressão numérica para v(t) quando t ≥ 0. b) Desenhe um gráfico de v(t) para o intervalo de tempo 0 ≤ t ≤
O resistor no circuito da Figura P8.11 é reduzido de 50 Ω para 40 Ω . Determine v 0 ( t ) para t ≥ 0 .
No circuito mostrado na Figura 8.1, um indutor de 20 mH está em paralelo com um capacitor de 500 nF, o resistor R está ajustado para amortecimento crítico e I 0 = 120 mA. a) Calcule o valor numérico d
Os elementos de circuito da Figura 8.1 são R = 125Ω , L = 200m H e C = 5μ F . A corrente inicial no indutor é -0,3 A e a tensão inicial no capacitor é 25 V.a) Calcule a corrente inicial em cada ramo d