a) Projete um circuito em série (veja a Figura 8.3) usando valores de componentes do Apêndice H, com uma frequência angular de ressonância de . Escolha um resistor ou crie uma rede de resistores de modo que a resposta seja criticamente amortecida. Desenhe seu circuito.
b) Calcule as raízes da equação característica para a resistência em (a).
Passo 1
Uooooooooooooooooooooooou! Salve, salve! Vamos para uma questãozinha de projeto que vai ter uma breve continuação na questão seguinte. É o seguinte, essa é uma daquelas questões que a gente tem que ficar olhando para o final do livro e voltando. Confesso que é um saco! Sendo assim, vamos facilitar as coisas.
a)
Sendo a frequência de ressonância , vamos olhar para a equação dela:
Pois bem, temos duas variáveis e apenas uma equação. Isso abre brecha para muitas possibilidades. Não podemos dizer “infinitas” porque os valores de resistência, indutância e capacitância dos componentes comerciais são limitados. Sendo assim, vai uma dica sobre o Apêndice H: Há 3 tabelas, 1 para resistores, 1 para indutores e 1 para capacitores. A tabela com indutores é a que possui menos valores, 4 especificamente. Então é melhor escolhermos um valor de indutância, e vermos se conseguimos um valor de capacitância que também está tabelado. Vamos escolher o seguinte valor: . Assim, a capacitância será dada por
Para o cálculo do resistor, vamos usar a relação . Como nos foi dito que a resposta tem que ser criticamente amortecida, temos que
Passo 2
Agora, temos que voltar para o apêndice e verificar se temos esses componentes disponíveis. Já adianto que não, o que significa que vamos ter que fazer associações. Das opções disponíveis, podemos usar 4 capacitores de em série que nos fornecerá uma capacitância cujo valor será ¼ desse valor. Além disso, para os resistores, podemos fazer a associação série de 2 resistores de e 1 resistor de . Isso será mostrado na figura abaixo:
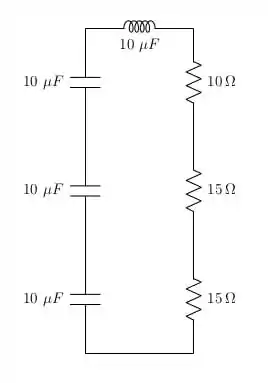
Passo 3
b)
As raízes da equação característica podem ser dadas pela equação
Como temos uma equação que vem de uma resposta criticamente amortecida, as raízes são repetidas e o valor é
Pois bem, finalizamos o que foi pedido, mas vamos para a próxima questão dar continuidade a essa questão delicinha de projeto.
Resposta
a)
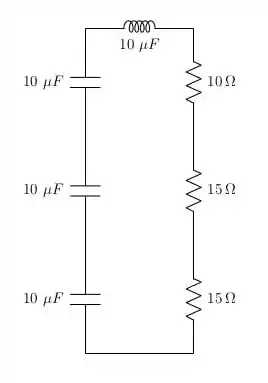
b)