Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.3 - Ex. 1
Calcule a corrente em regime permanente.
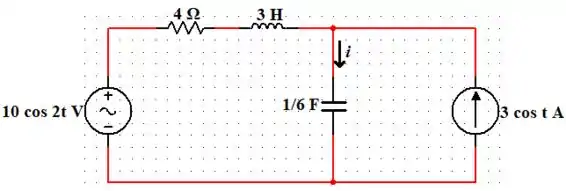
Passo 1
Falaeee!!
COMO ASSIM DUAS FREQUÊNCIAS DIFERENTES????
Caaaaaaalma!!! Seguinte... Aqui a gente vai usar o teorema da superposição. De forma resumida, vamos calcular separadamente as correntes que passam pelo capacitor e depois somá-las de tal forma que:
Passo 2
Para o primeiro caso vamos levar em conta apenas a fonte de tensão e devemos considerar a fonte de corrente como um circuito aberto.
Assim, vamos colocar em forma polar a fonte de tensão e vamos enxergar o indutor e o capacitor como reatâncias.
Lembrando que:
Em que, para esse caso, rad/s.
Logo, temos:
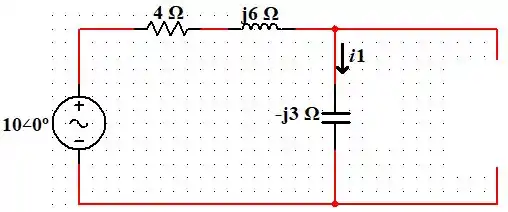
Assim fica muito fácil determinar a corrente pois:
Passo 3
Agora vamos desligar a fonte de tensão e considerá-la como um curto circuito. Vamos também considerar rad/s. Assim, colocando as reatâncias e deixando a fonte de corrente na forma polar, o circuito fica da seguinte forma:
Aplicando a Lei das Malhas, temos:
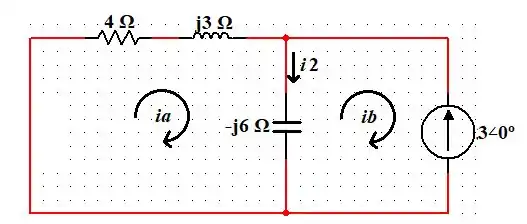
Na malha :
Na malha :
Substituindo o valor de na equação da malha :
Logo, é dada por:
Passo 4
Agora é só somar os valores de e :