Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.Problemas - Ex. 12

Calcule a corrente i em regime permanente.

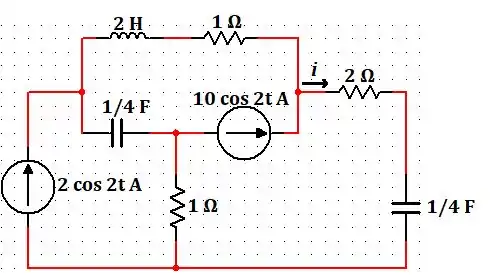
Passo 1

Falaeee!! Seguinte... Vamos primeiro passar os valores das fontes para a forma polar e enxergar os capacitores e o indutor em forma de reatâncias.

Lembrando que:

X_C = - (j)/(omega C)

X_L = j omega L

Em que omega = 2 r a d // s .

Logo, temos:

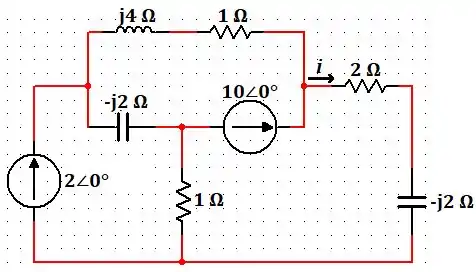
Passo 2

Podemos descobrir o valor de i aplicando o teorema da superposição. Vc faz primeiro a corrente do circuito somente abastecido pela fonte de 2 /_ 0 ° A e depois faz a mesma coisa somente com a fonte de 10 /_ 0 ° A . Aí por fim a gente soma os dois valores de corrente!!

Ficou confuso?? Então vem aqui ;)

Primeiro vamos fazer com a fonte de 2 /_ 0 ° A :

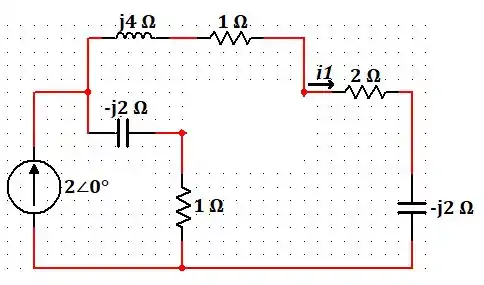
Aplicando o divisor de corrente, temos que:

i 1 = 2 xx ((1 - j 2))/((1 - j 2) + (j 4 + 1 + 2 - j 2)) :.

i 1 = 0.5 - j A

Passo 3

Agora, para a fonte de 10 /_ 0 ° A :

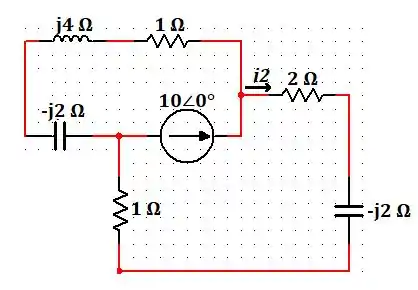
Aplicando o divisor de corrente, temos que:

i 2 = 10 xx ((1 + j 4 - j 2))/((1 + j 4 - j 2) + (2 - j 2 + 1)) :.

i 2 = 2 . 5 - j 5 A

Passo 4

Assim, temos que a corrente i é dada por:

i = i 1 + i 2 :.

i = 3 + j 4 :.

i = 5 cos (2 t + 53.13 °) A

Resposta

i = 5 cos (2 t + 53.13 °) A

Exercícios de Livros Relacionados

42. Considere a Figura 10.87 e elabore um problema para ajudar outros estudantes a entender melhor o teorema da superposição.
44. Use o princípio da superposição para obter v x no circuito da figura 10.89 . Seja v s = 50 sen ⁡ 2 tV e i s = 12 cos ⁡ ( 6 t + 10 ° )A .
43. Usando o princípio da superposição, determine i x no circuito da figura 10.88
45. Use superposição para determinar i ( t ) no circuito da figura 10.90
46. Determine v 0 ( t ) no circuito da figura 10.91 usando o princípio da superposição.