Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.8 - Ex. 3
Calcule ,a corrente em regime permanente, usando fasores
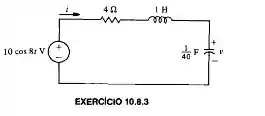
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Bem, vamos lá, primeiramente, vamos analisar os parâmetros de fase e frequência do circuito, para o caso da frequência, vamos relembrar a seguinte fórmula
Analisando essa mesma fórmula, nós temos que na fonte de tensão podemos destacar os seguintes parâmetros
Com isso, já podemos converter os componentes do domínio do tempo para o domínio da frequência, logo
Agora, podemos partir para o segundo ponto da nossa análise.
Passo 2
Veja que todos os componentes (Resistor, capacitor e indutor) estão em série, logo, podemos obter uma impedância afim de facilitar nossos cálculos para termos a corrente , com isso, nós temos que
Convertendo este valor para coordenadas polares
Logo, a corrente é igual a
Voltando para o domínio do tempo, nós obtemos o seguinte resultado