Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.1 - Ex. 1

Faça R   =   4     Ω , L   =   1 / 10   H e C   =   1 / 40   F na Fig. 15.1 e calcule a amplitude máxima e o ponto onde ela ocorre. Esboce também as respostas em amplitude e fase.

Passo 1

Faaaala, galera! Temos o seguinte circuito para resolver com base nos dados do enunciado:

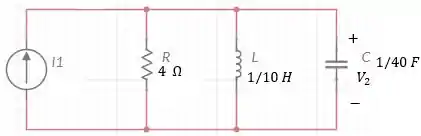
Temos um circuito RLC paralelo, logo podemos calcular a impedância por:

H s = V 2 ( s ) I 1 ( s ) = Z s = 1 1 R + s C + ( 1 / s L )

Podemos então obter a expressão para H s , reescrevendo a expressão obtida acima, da seguinte forma:

H s = 1 1 R + s C + ( 1 / s L )                       ( 1 )

Passo 2

Podemos também reescrever para obter a expressão na forma de equação característica. Logo, multiplicando tudo por 1 C s , obtemos:

H s = ( 1 / C ) s s 2 + ( 1 / R C ) s + ( 1 / L C )                 ( 2 )

Passo 3

Para s = j ω , substituindo em ( 1 ) :

H j ω = 1 1 R + j ω C + ( 1 / j ω L )

H j ω = 1 1 R + j [ ω C - ( 1 / ω L ) ]                       ( 3 )

Passo 4

Temos que ω = ω 0 quando:

ω C - 1 ω L = 0           ( 4 )

Logo:

ω 0 0,025 - 1 ω 0 0,1 = 0

ω 0 = ± 20

Passo 5

Temos que a amplitude é dada pelo modulo de H ( s ) , logo:

| H j ω | = 1 1 R 2 + [ ω C - ( 1 / ω L ) ] 2       = 1 1 R 2 + [ ω C - ( 1 / ω L ) ] 2        

H j ω = 1 1 4 2 + [ 0 ] 2        

H j ω = 1 0,0625 = 1 0,25 = 4      

| H j ω | = 4        

Passo 6

| H j ω | m á x = H j ω 0 = R = 4

Prontinho!

Resposta

| H j ω | m á x = H j ω 0 = R = 4

ω 0 = 20

Exercícios de Livros Relacionados

Calcule V_2 // V_g , para o circuito mostrado abaixo.
Para o circuito R L C em serie com uma fonte de tensão v g , faça a função de rede ser H=I / V g , ondeI e a corrente fasorial. Mostre que as respostas em amplitude e fase são similares as da Fig. 15.
Com o uso da Tabela 14.1, calcule as condições de (a) os parâmetros h (b) os parâmetros de transmissão, para esse circuito ser recíproco ( Z 12 = Z 21 ) .
Um segundo conjunto de parâmetros de transmissão pode ser definido. exprimindo as variáveis de saída em termos das variáveis de entrada, por V 2 = a V 1 - b I 1 I 2 = c V 1 - d I 1 Calcule os parametr