Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.Problemas - Ex. 6
Calcule R e L na Fig. 10.4, se a fonte é e a resposta é . (Tome .
Passo 1
Faaala, galerinha!! Como vocês estão? Partiu resolver mais uma questãozinha?
Para essa questão aqui, adotaremos o seguinte circuito:
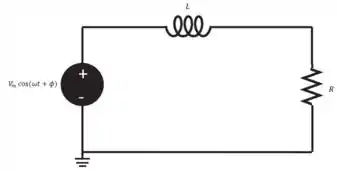
Passo 2
Agora, a partir do circuito apresentado no passo 1, podemos afirmar que a corrente I é:
Porém, para esse caso aqui, utilizaremos a mesma fórmula, mas na seguinte configuração alternativa:
Além disso, adotaremos também a seguinte fórmula:
Passo 3
Agora que determinamos as fórmulas que serão utilizadas para esse exercício, podemos seguir para os cálculos.
Primeiramente, elevaremos os dois lados da fórmula ao quadrado, para que esta fique da seguinte maneira:
Em seguida, sabemos do enunciado que = 67,4°, portanto, podemos isolar R a partir da fórmula :
Passo 4
Desenvolvendo a equação podemos obter o valor de L da seguinte maneira:
Agora que encontramos o valor de L, podemos somente substitui-lo na equação , de modo a obter o valor final de R:
Prontinho, pessoal!! Bora resolver mais uma questão juntos?