Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.Problemas - Ex. 7

Na Fig. Do Ex. 10.2.2, se a fonte é 6 cos ⁡ 4000 t   m A e a saída é v = 18 cos ⁡ 4000 t - 53,1 °   V , calcule R e C.

Passo 1

Faaala, galerinha!! Como vocês estão? Partiu resolver mais uma questãozinha?

Para essa questão aqui, adotaremos o seguinte circuito:

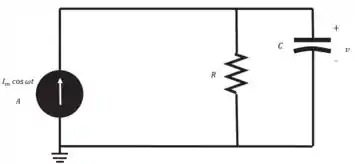
Passo 2

Agora, a partir do circuito apresentado no passo 1, podemos afirmar que:

I   ∠   0 ° = V   ∠ - 53,1 ° R + v j ω C

I R   ∠   0 ° = V   ∠ - 53,1 °   1 + j ω R C

I R v ∠ 53,1 ° = 1 2 + ω R C 2 tan - 1 ⁡ ω R C 1

10 - 3 3 R   ∠   53,1 ° = 1 2 + ω R C 2 tan - 1 ⁡ ( ω R C )   ( I )

Passo 3

Logo, a partir da equação desenvolvida no passo anterior, podemos isolar o valor de C da seguinte maneira:

53,1 ° = tan - 1 ⁡ ω R C

ω R C = tan ⁡ 53,1 °

R C = tan ⁡ 53,1 ° ω

R C = 3,33 * 10 - 4

C = 3,33 * 10 - 4 R   ( I I )

Passo 4

Agora, podemos elevar os dois lados da equação ( I ) ao quadrado, de modo a isolar-se R. Sendo assim, teremos:

10 - 6 R 2 9 = 1 + ω 2 R 2 C 2

Substituindo o valor de C encontrado no item anterior (equação I I ) temos:

10 - 6 R 2 9 = 1 + ω 2 R 2 3,33 * 10 - 4 R 2

R = 9 [ 1 + 4000 2 3,33 * 10 - 4 2 10 - 6 = 4,997   k Ω

Passo 5

Por fim, podemos substituir o valor de R encontrado no passo 4, na equação ( I ) , de modo a se obter o valor numérico de C:

C = 3,33 * 10 - 4 4,997 * 10 3 ~   6,66 * 10 - 8 F = 1 15 μ F

Prontinho, pessoal!! Bora resolver mais uma questão juntos?

Resposta

R = 4,997   k Ω   e   C = 6,66 * 10 - 8   F = 1 15   μ F

Exercícios de Livros Relacionados

Calcule os números complexos a seguir e deixe seus resultados na forma polar: 5 ∠ 30 ° 6 - j 8 + 3 ∠ 60 ° 2 + j 10 ∠ 60 ° 35 ∠ - 50 ° 2 + j 6 - ( 5 + j )
Calcule os números complexos a seguir e expresse seus resultados na forma retangular: 60 ∠ 45 ° 7,6 - j 10 + j 2 32 ∠ - 20 ° ( 6 - j 8 ) ( 4 + j 2 ) + 20 - 10 + j 24 20 + ( 16 ∠ - 50 ° ) ( 5 + j 12 )
Determine os fasores correspondentes aos seguintes sinais: v t = 21 cos ⁡ 4 t - 15 °V i t = - 8 s e n10 t + 70 °m A v t = 120 s e n10 t - 50 °V i t = - 60 cos ⁡ ( 30 t + 10 ° )m A
Determine os fasores correspondentes aos seguintes sinais: v t = 21 cos ⁡ 4 t - 15 °V i t = - 8 s e n10 t + 70 °m A v t = 120 s e n10 t - 50 °V i t = - 60 cos ⁡ ( 30 t + 10 ° )m A
Elabore um problema para ajudar outros estudantes a entender melhor os fasores.