Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 34
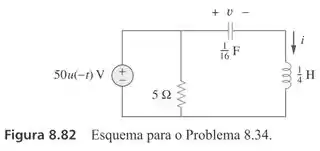
Calcule i(t) para t > 0 no circuito da Figura 8.82.
Passo 1
Antes de t = 0, o capacitor age como um circuito aberto, enquanto o indutor se comporta como um curto-circuito. Então:
Passo 2
Para t > 0, o circuito LC é desconectado da fonte de tensão, como mostra a figura abaixo.
Este é um circuito RLC em série sem perdas e sem fonte. Vamos calcular os valores de α, ω0 e S.
Passo 3
Como α é igual a zero, temos uma resposta sub-amortecida. Portanto:
Aplicando t = 0, encontramos:
Passo 4
Agora só falta encontrar o A2. Vamos continuar analisando o caso para t = 0:
Como já sabemos que A1 = 0, então:
Resposta
Exercícios de Livros Relacionados
Calcule x , se d 2 x d t 2 + 25 x = 0
Se a tensão nodal no nó b da Fig. 9.3 é v 1 , mostre que as duas equações nodais são v - v g 4 + v - v 1 R + 1 4 d v d t = 0 E v 1 - v g R + ∫ 0 t v 1 d t + i 0 = 0 Diferencia a segunda destas equaçõe
Calcule a resposta forçada se d 2 x d t 2 + 4 d x d t + 3 x = f t Onde f ( t ) é dada por a6 ,b 8 e - 2 t ,c 6 t + 14 .
Se x 0 = 4 e d x 0 d t = - 2 , calcule a solução completa no Ex. 9.5.1.
Calcule a resposta completa se d 2 x d t 2 + 9 x = 18 s e n 3 t E x 0 = d x 0 d t = 0 Sugestão: Verifique x f = t ( A c o s 3 t + B s e n 3 t )