Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 35
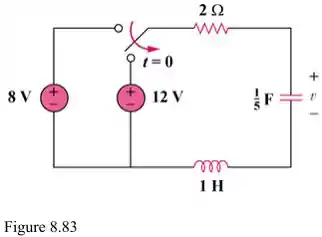
Determine v(t) para t > 0 no circuito da Figura 8.83.
Passo 1
Vamos seguir o passo a passo do sucesso para responder esse tipo de questão. Primeiro analisaremos o circuito quando t = 0-:
Como sabemos, antes de t = 0, o capacitor age como um circuito aberto, enquanto o indutor se comporta como um curto-circuito. Então:
Passo 2
Para t > 0, teremos um circuito RLC série. E o que devemos fazer nesse caso?
Isso mesmo, devemos calcular α, ω0 e S.
Como α
Passo 3
Conhecendo os valores de e podemos iniciar a montagem da equação de resposta natural.
Nos resta agora encontrar A e B. Fazendo t = 0:
Passo 4
Fazendo:
Ao aplicar t = 0, encontramos:
Resposta
Exercícios de Livros Relacionados
Calcule a resposta forçada se d 2 x d t 2 + 4 d x d t + 4 x = f t Onde f ( t ) é dado por (a) 6 e - 2 t , (b) 6 t e - 2 t .Sugestão: Em (b), tente x f = A t 3 e - 2 t
Calcule a resposta forçada se d 2 x d t 2 + 4 d x d t + 3 x = f t Onde f ( t ) é dado por (a) 2 e - 3 t + 6 e - 4 t , (b) 4 e - t + 2 e - 3 t
Calcule x , t0 , onde d x d t + 2 x + ∫ 0 t x d t = f t x 0 = - 1 E ( a ) f t = 1 e b f t = t 2
Calcule v para t0, se 0 circuito esta em regime permanente em t = 0.
Para o circuito do Exemplo 8.8, determine v ( t ) para t ≥ 0.