Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Problemas - Ex. 28

Um circuito R L C em série é descrito por

L d 2 i   d t 2 + R d i d t + i C = 10  

Determine a resposta quando L = 0,5   H , R = 4   Ω e C = 0,2   F . Considere i 0 = 1 e d i 0 d t = 0 .

Passo 1

Relaxa, galera. Vamo se Ligar e achar a Resposta. Questão bem de boas. Temos que a equação caracteristica é

L s 2 + R s + 1 C = 0 → 1 2 s 2 + 4 s + 1 0.2 = 0 → s 2 + 8 s + 10 = 0

s 1,2 = - 8 ± 64 - 40 2 =   - 6.45   e - 1.5505

Logo,

i t = i s + A e - 6.45 t + B e - 1.5505 t

Passo 2

Mas ai a gente lembra que:

i s / C = 10 ou i s = 0.2 × 10 = 2

i t = 2 + A e - 6.45 t + B e - 1.5505 t

Aplicando para t=0,

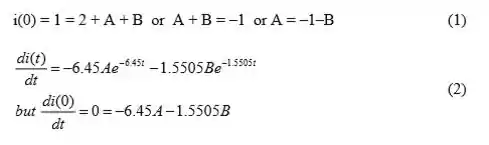
Portanto,

i t = 2 - 2.3163 e - 6.45 t - 1.3163 e - 1.5505 t A

Resposta

i t = 2 - 2.3163 e - 6.45 t - 1.3163 e - 1.5505 t A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No circuito da Figura 8.104 , a chave se encontra na posição 1 há um longo tempo, porém, muda para a posição 2 em t = 0 . v 0 + , d v 0 + d t v t para t ≥ 0 .
Para o circuito da Figura 8.101 , detemrine v ( t ) para t0 . Suponha v 0 + = 4V e i 0 + = 2A .
Para o circuito do problema 8.5 , determine i e v pata t0 .
Se a chave na figura 8.103 se encontrar desligada há um longo tempo antes de t = 0 , porém é aberta em t = 0 , determine:A equação característica do circuito. i X e v R para t0 .
Obtenha i_1 e i_2 para t0 no circuito da Figura 8.106 .