Calcule a potência entregue aos resistores de da Fig. 5.8 (a) e da Fig. 5.8 (b) e mostre que a sua soma não é igual a potência total entregue ao resistor de na Fig. 5.7.
Passo 1
E aí, galerinha! Tudo tranks? Simbora pra mais uma aí!?
Bom! Temos o seguinte circuito na figura
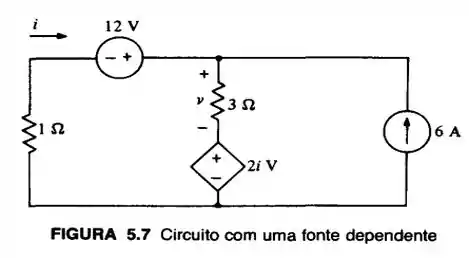
E para o resistor de desse circuito, foi determinado uma potência dada por...
Agora, vamos ver como se sairia a potência para o resistor de se usássemos o método da superposição...
Temos duas fontes independentes aí, a fonte de tensão contínua de e a fonte de corrente de . Para usar a superposição, vamos ter que calcular como seriam essas duas fontes separadas!
Passo 2
Para a primeira parte, vamos excluir a fonte de corrente de ... Com isso, temos que...
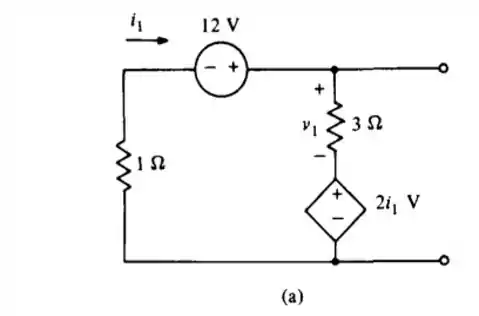
Aplicando a análise de malha, temos que...
E então, fica fácil a gente achar a potência no resistor de ... Basta aplicar a fórmula ...
Passo 3
Para a segunda parte do circuito, vamos excluir a fonte de ... Com isso, temos que...
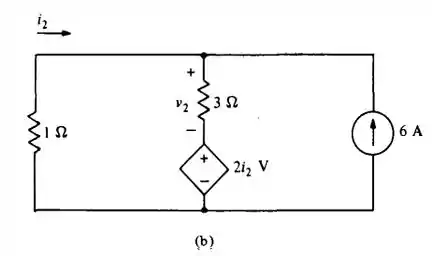
Aplicando novamente a ... E sabendo que a tensão é a mesma nos ramos, obtemos que...
Isso que dizer que a corrente flui no sentido contrário ao que estipulamos! Mas de qualquer forma, o valor da corrente continua sendo o mesmo e igual a ! A corrente circulando no resistor de , será então dada pela subtração de e ... Calculando dessa forma, a potência...
Pronto! Agora, vamos somar as duas potências obtidas...
Viu só! Passou foi longe do verdadeiro valor de potência total entregue ao resistor de , determinado na figura 5.7