Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 11
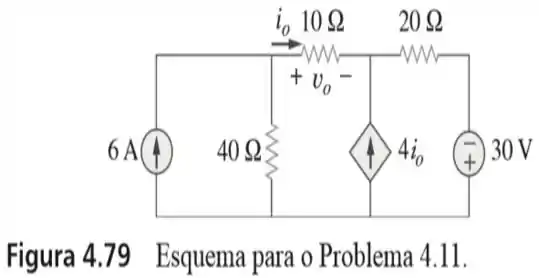
11. Use o princípio da superposição para determinar e no circuito da figura
Passo 1
Olha só! No circuito da figura do enunciado, há a presença de duas fontes independentes; uma fonte de tensão de e uma fonte de corrente de .
Logo, usando superposição, temos que a tensão é dada pela soma das contribuições de tensão das três fontes individualmente. No caso, chamaremos de a contribuição da fonte de corrente e de a contribuição da fonte de tensão.
Passo 2
Primeiro, vamos determinar . Para isso, vamos retirar a fonte de tensão, substituindo por um curto-circuito.
De modo que nosso circuito passa a ter a seguinte cara:
Fazendo a análise nodal para o nó :
E depois, para o nó :
Substituindo em , obtemos que:
E o valor de é dado por:
Obtemos desse modo, olhando o circuito da figura acima que a tensão equivale a diferença entre e ... Desse jeito aqui:
Passo 3
Em seguida, vamos determinar . Para isso, vamos substituir a fonte de corrente por um circuito aberto e deixar apenas a fonte de tensão presente.
E o circuito fica desse jeito aqui:
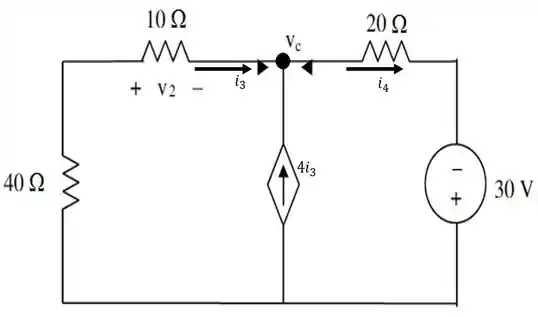
Aplicando a análise nodal pro nó desse circuito, obtemos que:
A tensão , que a gente tanto procura, é dada olhando a figura acima, por:
Como já sabemos o valor de ... Aí fica moleza achar a resposta:
Passo 4
Pra finalizar, basta somar e e e encontraremos ...
Para achar o valor da corrente , só é preciso dividir essa tensão pela resistência presente no circuito completa, que é igual a ...
E voilà! Respostas encontradas.