Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.3 - Ex. 2
Calcule a resposta forçada , se e .
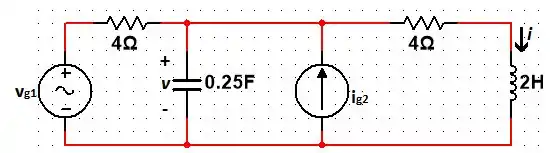
Passo 1
Eaeee!! Beleza? Vamos para mais uma aqui!!
Como as frequências complexas são diferentes, vamos utilizar o teorema da superposição. Em que:
Passo 2
Também sabemos que, para uma resistência , a impedância é:
Para uma indutância , sua impedância é:
E, para uma capacitância , sua impedância é:
Nesse sentido, para o circuito desse exercício, temos:
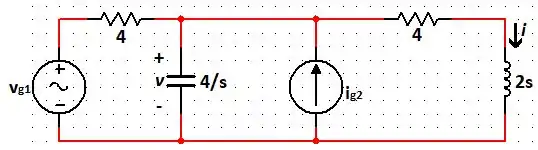
Passo 3
Fazendo primeiro com a fonte de tensão, temos:
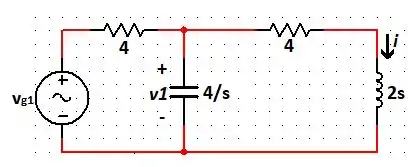
Por divisor de tensão, temos que é dado por:
Passo 4
Para este caso, sabemos que:
Assim, substituímos em :
Passo 5
Agora, para a fonte de corrente, temos:
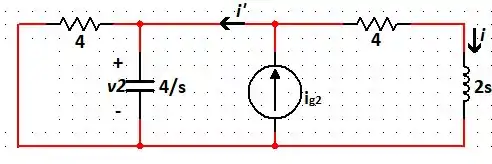
Fazendo a Lei dos Nós, temos:
Passo 6
Para este caso, sabemos que:
Assim, substituímos em :
Passo 7
Portanto, somando as duas tensões, temos:
Resposta
Exercícios de Livros Relacionados
D a d aaf u n ç ã od er e d e çã H ( s ) = V o ( s ) V i ( s ) = 4 s ( s + 2 ) ( s + 1 ) ( s + 3 ) Se nāo ocorrer nenhum cancelamento, calcule a resposta completa v i ( t ) , para t0 , se vi(t = 6 e '
Calcule a resposta completa v para t0 , usando a funçāo de rede, se v 0 * e d v 0 + / d t sāo iguais a zero
Mostre que, para a Fig. 14.16, em função dos parâmetros de transmissão, temos V 2 V 1 = 1 A + B Confira o resultado, usando essa fórmula para a rede com o resistor do Prob. 14.32
Execute as operações indicadas a seguir para formas de onda não-senoidais:a. 60 + 70 s e n ω t + 20 s e n 2 ω t + 90 ∘ + 10 s e n 3 ω t + 60 ∘ + [ 20 + 30 s e n ω t - 20 c o s 2 ω t + 5 c o
Determine a corrente i s no circuito visto na Figura 25.37 . i 2 = 10 + 30 s e n 20 t - 0,5 s e n 40 t + 90 ∘ i 1 = 20 + 4 s e n 20 t + 90 ∘ + 0,5 s e n 40 t + 30 ∘