Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.Problemas - Ex. 33

Mostre que, para a Fig. 14.16, em função dos parâmetros de transmissão, temos

V 2 V 1 = 1 A + B

Confira o resultado, usando essa fórmula para a rede com o resistor do Prob. 14.32

Passo 1

O enunciado pede para calcularmos , usando essa fórmula para a rede com o resistor do Prob. 14.32.

Esboce o circuito primeiramente

V 1 = A V 2 - B I 2

I 1 = C V 2 - C I 2

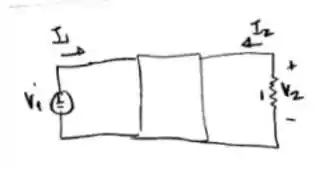
Temos que I 2 = - V 2

V 1 = A V 2 + B V 2

V 1 = ( A + B ) V 2

v 2 v 1 = 1 A + B

Resposta

v 2 v 1 = 1 A + B

Exercícios de Livros Relacionados

Determine v ( t ) nas seguintes equações integro-diferenciais usando o método de fasores: v t + ∫ v d t = 10 cos ⁡ t d v d t + 5 v t + 4 ∫ v d t = 20 s e n ( 4 t + 10 ° )
Aplique análise fasorial para calcular o seguinte: v = 110 sen ⁡ 20 t + 30 ° + 220 cos ⁡ 20 t - 90 °V i = 30 cos ⁡ 5 t + 60 ° - 20s e n 5 t + 60 °A
Usando fasores, determine i ( t ) nas seguintes equações: 2 d i d t + 3 i t = 4 cos ⁡ ( 2 t - 45 ° ) 10 ∫ id t + d i d t + 6 i t = 5 cos ⁡ ( 5 t + 22 ° )
Um circuito R L C em paralelo possui a equação nodal a seguir: d v d t + 50 v + 100 ∫ vd t = 100 cos ⁡ ( 377 t - 10 ° )V Determine v ( t ) usando o método fasorial. Supondo que o valor da integral em
Um circuito R L C série tem R = 80Ω , L = 240m H e C = 5m F . Se a tensão de entrada for v t = 10 cos ⁡ 2 t determine a corrente que flui através do circuito.