Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.3 - Ex. 1

Calcule a resposta forçada i , se v_g = 4 e^(- t) cos t V .

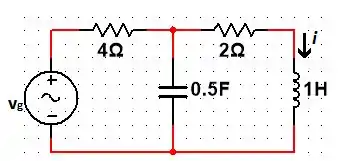
Passo 1

Faaala meu/minha consagrado(a)!! Beleza?

Sabendo que v_g = 4 e^(- t) cos t , temos que:

V_g (s) = 4 /_ 0 ° V

Passo 2

Também sabemos que, para uma resistência R , a impedância é:

Z_R (s) = R

Para uma indutância L , sua impedância é:

Z_L (s) = s L

E, para uma capacitância C , sua impedância é:

Z_C (s) = (1)/(s C)

Nesse sentido, para o circuito desse exercício, temos:

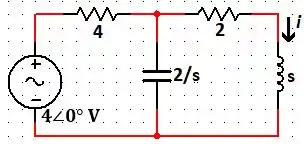
Passo 3

Aplicando a Lei dos Nós, temos:

(4 /_ 0 ° - v)/(4) = (v)/(2 // s) + (v)/(2 + s) :.

v = V ( s ) = (8 s + 16)/(4 s^2 + 1 0 s + 12)

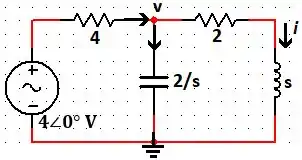
Assim, temos que I ( s ) é dado por:

I (s) = (V (s))/(2 + s) :.

I (s) = ((8 s + 16)/(4 s^2 + 10 s + 12))/(2 + s) :.

I (s) = (8 s + 16)/(4 s^3 + 18 s^2 + 32 s + 24)

Passo 4

Sabemos que:

s = - 1 + j

Assim, substituímos em I ( s ) para encontrarmos i :

i = (8 ( - 1 + j ) + 16)/(4 ( - 1 + j )^3 + 18 ( - 1 + j )^2 + 32 ( - 1 + j ) + 24) :.

i = (8 + j 8)/(j 4) :.

i = 2 - j 2 :.

i = 2 sqrt(2) /_ - 45 ° A

Ou

i = 2 sqrt(2) e^(- t) cos (t - 45 °) A

Gostou da questão?? Vamos para outra!!

Resposta

i = 2 sqrt(2) e^(- t) cos (t - 45 °) A

Exercícios de Livros Relacionados

Calcule v ( t ) se (a)V = 4 /_ 0 ° , s = - 3 ; (b)V = 5 /_ 15 ° , s = j 2 e (c)V = 5 /_ 3 0 ° , s = - 3 + j 2 .
Calcule a resposta forçada v , se v_g 1 = 4 e^(- 2 t) cos ( t - 45 ° ) V e i_g 2 = 2 e^(- t) A .
Para o circuito do Ex. 14.3.2, tome i g 2 = e - 2 t c o s ⁡ ( t + 45 ° ) A, permanecendo v g 1 como está, e calcule v por (a)usando superposição, (b) escrevendo uma única equação de nó e (c) usando tr
Dada a função de rede H s = 4 s + 5 s 2 + 4 s + 5 E a entrada V i s = 2 ∠ 0 ° Calcule a resposta forçada v 0 ( t ) se (a) s = - 2 , (b) s = - 4 + j 1 e (c) s = - 2 + j 3 .