Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 14.3 - Ex. 3
Para o circuito do Ex. 14.3.2, tome A, permanecendo como está, e calcule por (a)usando superposição, (b) escrevendo uma única equação de nó e (c) usando transformações de fonte.
Passo 1
Bom dia, boa tarde, boa noite, boa madrugada!! Vamos para mais umazinha!!
Temos o seguinte circuito:
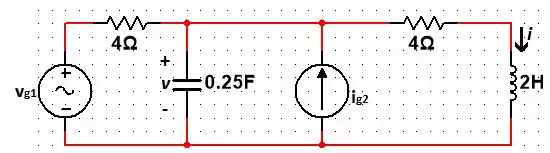
Vamos primeiro utilizar a superposição para encontrar . Assim, temos que:
Passo 2
Também sabemos que, para uma resistência , a impedância é:
Para uma indutância , sua impedância é:
E, para uma capacitância , sua impedância é:
Nesse sentido, para o circuito desse exercício, temos:
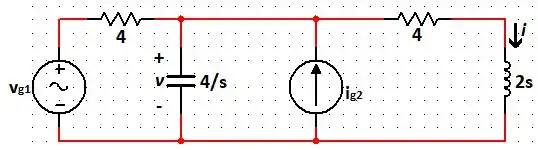
Passo 3
Fazendo primeiro com a fonte de tensão, temos:
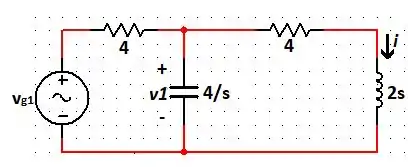
Por divisor de tensão, temos que é dado por:
Passo 4
Para este caso, sabemos que:
Assim, substituímos em :
Passo 5
Agora, para a fonte de corrente, temos:
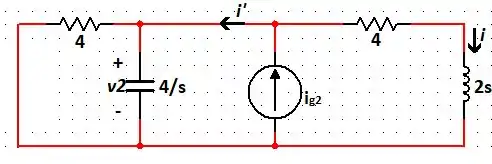
Fazendo a Lei dos Nós, temos:
Passo 6
Para este caso, sabemos que:
Assim, substituímos em :
Passo 7
Portanto, somando as duas tensões, temos:
Passo 8
Fazendo uma única equação de nó, temos:
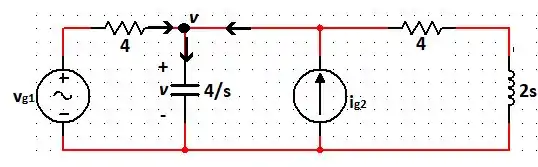
Sabemos que , e . Logo, temos:
Passo 9
Usando transformações de fonte, temos:
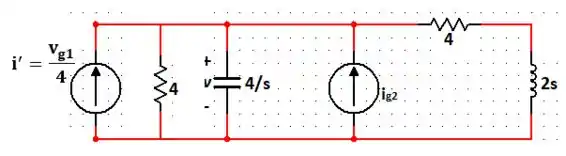
Passo 10
Fazendo a Lei dos Nós, temos:
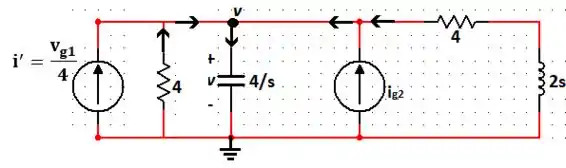
Fazendo , e , temos que:
Ufaaaa! Vamos para outra!! ;)