Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 39

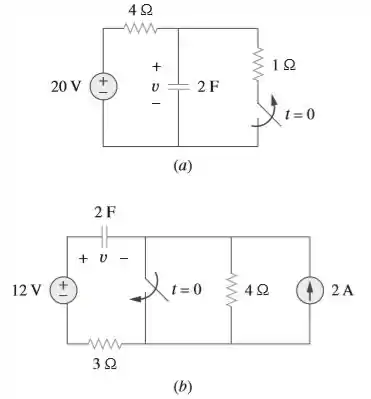
Calcule a tensão no capacitor para t < 0 e t > 0 para cada um dos circuitos da Figura 7.106.

Passo 1

Certo pessoal, vamos lá! Temos dois momentos pra analisar, em dois circuitos diferentes. O importante nesse tipo de questão é saber analisar as tensões em cada malha, se atentando se a chave vai abrir ou fechar em t = 0 ! (não vacilem nisso, ok?)

Para a letra a ) temos que para antes de t = 0

v t = 1 4 + 1 20 = 4 V

Legal! Vamos para depois de t = 0 .

Passo 2

Depois de t = 0 temos o nosso esqueminha da formula de EDO para o circuito! Facinho galera, vamos la!

v t = v ∞ + v 0 - v ∞ e - t / τ

Mas sabemos que,

τ = R C = 4 2 = 8

v 0 = 4 V , v ∞ = 20 V

Daí é so jogar na fórmula!

v t = v ∞ + v 0 - v ∞ e - t / τ

v t = 20 + 4 - 20 e - t / 8

Logo,

v t = 20 - 16 e - t 8     V

Passo 3

Entenderam o esquema? Vamos usar o mesmo fundamento para a letra b ) , mudando algumas coisinhas. Antes de t = 0 , temos que v = v 1 + v 2 (Onde v 1 é devido a fonte de 12V e v 2 devido a fonte de 2A). Então simbora descobrir esse v 2 né? Transformando a fonte de corrente em de tensão, temos que:

Ou seja, v 2 é igual a -8 (adotando o mesmo sentido de v 1 ). Logo,

v = 12 - 8 = 4 V

Passo 4

Vamos agora trabalhar depois de t = 0 ! O nosso circuito vai simplificar bastante, ficando assim:

Logo,

v t = v ∞ + v 0 - v ∞ e - t / τ

v ∞ = 12 V ,   v 0 = 4 V

τ = R C = 2 3 = 6

Logo,

v t = 12 + 4 - 12 e - t / 6

v t = 12 - 8 e - t / 6 V

Resposta

a A n t e s   d e   t = 0 → v t = 4 V ,   d e p o i s   d e   t = 0 → v t = 20 - 16 e - t 8     V

( b ) A n t e s   d e   t = 0 → v t = 4 V ,   d e p o i s   d e   t = 0 → v t = 12 - 8 e - t / 6 V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um circuito de antena sintonizado em série é formado por um capacitor variável ( 40p F a 360p F ) e uma bobina de antena de 240μ H que possui uma Resistência C C igual a 12Ω .Determine o intervalo de
O circuito de cruzamento da figura é um filtro passa altas conectado a um tweeter. Determine a função de transferência H ω = V 0 ω / V i ω .
O circuito de cruzamento da figura é um filtro passa-baixas conectado a um woofer. Determine a função de transferência H ω = V 0 ω / V i ω .
Determinando circuito eletrônico para teste produziu uma curva ressonante com pontos de meia potência em 432 H z e 454 H z . Se Q = 20 , qual é a frequência de ressonância do circuito?
Um filtro passa-faixa de dupla sintonia e baixo fator de qualidade é mostrado na figura. Use PSpice ou MultiSim para gerar o gráfico de amplitude de V 0 ω .