Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.9 - Ex. 4
Calcule a tensão em regime permanente , usando circuito fasorial dado que .
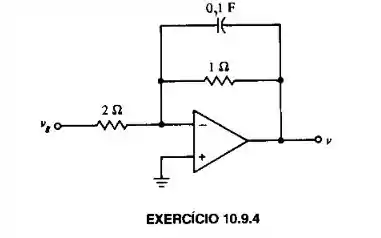
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Convertendo para fasores, ele fica da seguinte forma
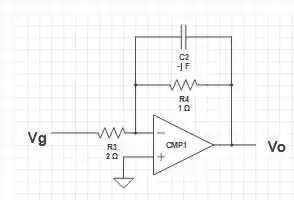
Basicamente, esse OPAMP vai funcionar como um “inversor”, por causa do aterramento, ok, isso em “matematiquês” é igual a
Logo, é igual a
Vamos considerar como a resistência equivalente entre o capacitor e o resistor de , com isso, nós temos que
Vamos brincar um pouco com essa equação
Passo 2
Desenvolvendo os termos, nós temos que
Um pouco mais...
Convertendo para fasores
Racionalizando
E no domínio do tempo, nós temos que
Resposta
Exercícios de Livros Relacionados
Calcule os números complexos a seguir e expresse seus resultados na forma retangular: 60 ∠ 45 ° 7,6 - j 10 + j 2 32 ∠ - 20 ° ( 6 - j 8 ) ( 4 + j 2 ) + 20 - 10 + j 24 20 + ( 16 ∠ - 50 ° ) ( 5 + j 12 )
Determine os fasores correspondentes aos seguintes sinais: v t = 21 cos 4 t - 15 °V i t = - 8 s e n10 t + 70 °m A v t = 120 s e n10 t - 50 °V i t = - 60 cos ( 30 t + 10 ° )m A
Determine os fasores correspondentes aos seguintes sinais: v t = 21 cos 4 t - 15 °V i t = - 8 s e n10 t + 70 °m A v t = 120 s e n10 t - 50 °V i t = - 60 cos ( 30 t + 10 ° )m A
Elabore um problema para ajudar outros estudantes a entender melhor os fasores.
Seja X = 4 ∠ 40 ° e Y = 20 ∠ - 30 ° . Calcule as quantidades a seguir e expresse seus resultados na forma polar. X + Y X * X - Y * ( X + Y ) / X