Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 12
a) Calcule a tensão a vazio do circuito divisor de tensão mostrado na FiguraP3.12.b) Calcule a potência dissipada em R1 e R2.c) Suponha que haja apenas resistores de 0,5 W disponíveis. A tensão a vazio deveser a mesma que em (a). Especifique os menores valores ôhmicos de R1 e R2.
Passo 1
Fala, galera! Beleza? Espero que sim. Bora fazer uma questão de divisor de tensão.
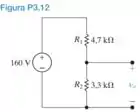
a) Para achar basta fazer uso da ferramenta divisor de tensão:
Passo 2
b)
Passo 3
c) Sabemos que a corrente que passa tanto em R1 quanto em R2 é a mesma, então:
E sabemos também que
Logo, podemos achar R2:
Resposta
a)
b)
c)R1 = 17.672
R2 = 12.408
Exercícios de Livros Relacionados
Determine a potência dissipada no resistor de 5 Ω no circuito divisor de corrente na Figura P3.16.
Especifique os resistores no circuito da FiguraP3.18 para atender aos seguintes critériosde projeto: i g = 50 m A ; v g = 25 V; i 1 = 0,6 ⋅ i 2 ;i 3 = 2 ⋅ i 2ei 4 = 4 ⋅ i 1
Para o circuito divisor de corrente da Figura 3.17, calcule:a) i o e v o .b) a potência dissipada no resistor de 6 Ω .c) a potência fornecida pela fonte de corrente.
A tensão a vazio no circuito divisor de tensão mostrado na Figura P3.14 é 8 V. O menor resistor de carga que está sempre ligado ao divisor é 3,6 k Ω . Quando o divisor estiver carregado, v o não dever
Um resistor de derivação e um medidor de d’Arsonval de 50 mV, 1 mA são usados paraconstruir um amperímetro de 5 A. Uma resistência de 20 m Ω é colocada nos terminais doamperímetro. Qual é a nova faixa