Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 4.Problemas - Ex. 30
Calcule v usando o método (nodal ou de malhas) que requer o menor número de equações.
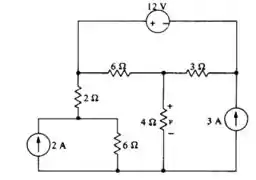
Passo 1
Falaa galerinhaa!!! Tudo tranquilo?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para o determinar . Puts!! Já parece difícil?? Vai ser tranquilo. Partiu??
Com a análise de malha nosso circuito ficará o seguinte
Agora já facilita muito a nossa visualização!!
Passo 2
Então bora láa!!
Vamos analisar esse circuito
Aplicando LKT na malha 2,no sentido horário, temos
Agora para a malha 3
Analisando a malha 1 e 4
Como só temos fonte de corrente independente, então
Passo 3
Agora vamos para o último passo!!
Substituindo os dados encontrados em (1), chegamos em
Agora em (2)
Como temos duas incógnitas para duas equações, conseguimos resolver!
Isolando uma incógnita em uma equação e substituindo na outra equação, temos
Como
Pronto!!