Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 61
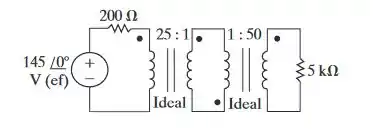
Determine a potência média fornecida ao resistor de 5 kV no circuito da Figura P10.61.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Como os transformadores ideais são sem perdas, a potência média fornecida ao resistor de é igual à potência média fornecida à impedância vista no enrolamento primário do transformador de relação de espiras .
Para o transformador de relação de espiras , temos as seguintes características:
- A relação entre a tensão do enrolamento primário Va e a tensão do enrolamento secundário é dada por
- E a relação entre a corrente em seu enrolamento primário e a corrente é igual a
Dividindo (1) por (2) para conseguir a impedância vista através dos terminais de enrolamento
Com isso, nós temos que
Passo 2
Para o transformador de relação de espiras (25:1), nós temos as seguintes relações
- A relação entre a tensão do enrolamento primário e a tensão do enrolamento secundário é dada por
- A relação entre a corrente e a corrente é dada por
Com isso, a impedância é dada por
Dividindo (3) por (4), nós obtemos o seguinte resultado
Fazendo a substituição
Passo 3
Conectando a impedância calculada nos terminais do enrolamento primário do transformador de relação de espiras (25:1) e os terminais c,d. Com isso, vamos determinar a corrente fluindo através da impedância
Com isso, nós temos que
Determinando a potência média P transferida para a impedância
Fazendo a devida substituição de valores, nós temos que
Com isso