Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 28
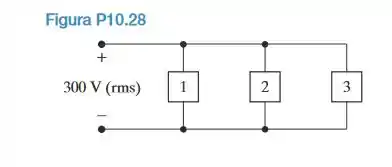
Três cargas estão ligadas em paralelo a uma linha de 300 V (ef), como mostra a Figura P10.28. A carga 1 absorve 3 kW com um fp unitário; a carga 2 absorve 5 kVA, com um fp adiantado de 0,8; a carga 3 absorve 5 kW e fornece 6 kVARs.
a) Determine a impedância equivalente das três cargas em paralelo.
b) Determine o fator de potência da carga equivalente, vista dos terminais de entrada da linha.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A – Primeiramente, a potência complexa da primeira carga é dada por
A potência complexa é dada por
Agora, nós vamos determinar a potência média na segunda carga
Substituindo os valores, nós temos que
Onde é a magnitude da potência complexa. Agora, falta determinar a potência reativa da segunda carga
Fazendo a substituição dos valores, nós temos que
Passo 2
A potência complexa é dada por
Determinando a potência total complexa fornecida das três cargas
Substituindo os valores, nós temos que
Agora, vamos para a corrente entregue as três cargas
Fazendo a substituição, nós temos que
Portanto
Passando para fasores, nós temos que
Agora, falta basicamente nada para calcular a resistência equivalente das cargas, com isso, nós temos que
Fazendo a substituição
Que será igual a
Na notação fasorial será igual a
Passo 3
B - A diferença de fase entre a tensão aplicada nas cargas e o circuito entregue a elas é dada por
Determinando o fator de potência da carga equivalente:
Logo, temos que
Como a corrente lidera a tensão, o fator de potência está adiantado