Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 37
a) Determine a potência média fornecida ao resistor de no circuito da Figura P10.37.
b) Determine a potência média produzida pela fonte de tensão senoidal ideal.
c) Determine .
d) Mostre que a potência média fornecida é igual à potência média dissipada.
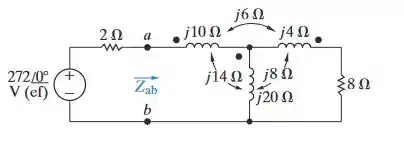
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A – Primeiramente, nós vamos escrever as duas equações das malhas, a primeira fica com o seguinte equacionamento
Rearranjando,
A segunda equação fica da seguinte forma
Novamente fazendo o rearranjo
Substituindo (2) em (1) para determinar
Portanto,
Substituindo em (2) para conseguir
Com isso, nós temos que
Que em fasores,
Determinando a potência média dissipada no resistor de
Substituindo os valores, nós temos que
Portanto,
Passo 2
B - Determinando a potência complexa desenvolvida pela fonte de tensão,
Fazendo a troca dos termos
Onde, o sinal negativo indica que a potência complexa é desenvolvida pela fonte. Determinando a potência média desenvolvida pela fonte de tensão
O sinal negativo indica que essa potência média é desenvolvida pela fonte de tensão
Passo 3
C – A impedância é igual a
Substituindo os valores, nós temos que
Que passando para fasores,
Passo 4
D - Determinando a potência média dissipada no resistor de
Com isso, nós temos que
A potência média total dissipada nos dois resistores é igual a
Substituindo os valores, nós obtemos o seguinte resultado
A potência média desenvolvida pela fonte de tensão é igual à potência média dissipada nos dois resistores