Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 19
Calcule para , se o circuito está em regime permanente em
Passo 1
Iae, galerinha. Tudo bem?
Já estão nível NASA que tlgd! Vamos fazer essa questão de circuito RL juntos? Dá só uma olhadinha no circuito que lindão! Mais uma vez, vamos dividir o circuito em duas partes: regime transitório e regime permanente. Partiu! 💪
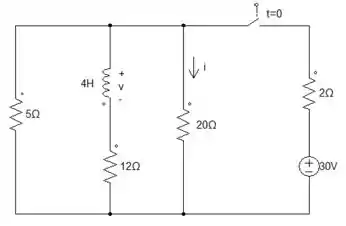
A princípio, vamos analisar o circuito em regime permanente, para isso temos que desconectar o indutor. Se liga como o circuito fica agora:
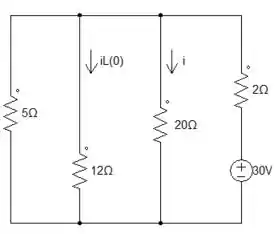
Show de bola! Agora, ficou fácil essa parte né? Precisamos achar a corrente equivalente, o , mas antes temos que fazer a associação dos resistores.
O resistor de 5Ω está em paralelo com o de 20Ω.
//
//
//
O resistor de 4Ω está em paralelo com o de 12Ω.
//
//
//
O resistor de está em série com o de .
= 3 + 2
= 5Ω
Passo 2
Belezinha! Como já sabemos nosso , vamos fazer lei de Ohm e descobrir nossa corrente total quando em regime permanente😉
Agora, que temos o para acharmos o , temos que fazer nosso já conhecido e amigo, o divisor de correntes.
Show de bolinhas! 😍Tá nível NASA já!
Passo 3
Boa, galera! Mandou muito bem na primeira parte. Agora, vamos fazer a análise de quando o circuito está em regime transitório. Se liga aí como ele fica 😉
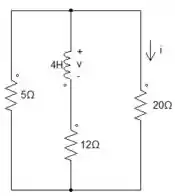
E aí, acertou como fica em regime transitório? Sei que sim! Então, vamos lá! Podemos observar que os resistores estão não estão associados, então vamos fazer juntinhos?
O resistor de 5Ω está em paralelo com o de 20Ω.
//
//
//
O resistor de está em série com o de .
= 4 + 12
= 16Ω
E, assim, fica nosso circuito equivalente em regime transitório:
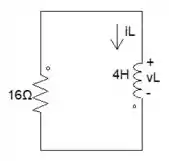
Passo 4
Nessa parte, vamos começar fazendo LKT e, assim, iremos achar nossa EDO. Vamos lá!
Como já sabemos, o , então:
Maravilha! Já achamos nossa EDO, vamos descobrir o agora.
Passo 5
Sensacional, pessoal! Estamos quase lá. O próximo passo agora, é sabermos qual a nosso Para isso, vamos usar a equação . lembrando que nosso . Vamos lá!
Show dmss! Super fácil né?! Blz, pessoal, feito isso, já podemos saber quanto é o
Lembra quanto vale nosso ? Tínhamos definido no Passo 4, que pela LKT . Sendo assim:
Passo 6
Ufaaa. Até que fim estamos no final. Só precisamos achar agora nosso e para isso, mais uma vez vamos usar divisor de corrente 😉 Show né não? Partiu!