Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 31

Não há nenhuma energia armazenada no circuito na Figura P13.31 no instante em que a fonte de corrente é aplicada.

a) Determine Ia e Ib.

b) Determine ia e ib.

c) Determine Va, Vb e Vc.

d) Determine va, vb e vc.

e) Admita que um capacitor se danificará sempre que sua tensão terminal for 1.000 V. Quanto tempo, após a fonte de corrente ter sido aplicada, um dos capacitores se danificará?

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!

  1. Podemos desenvolver o sistema mostrado acima como na seguinte ilustração:

    2. Disso tiramos um sistema de equações:

    10 s I 1 + 10 s I 1 - I 2 + 10 I 1 - 9 s = 0

    10 s I 2 - 9 s + 10 s I 1 - I 2 + 10 I 2 = 0

    Inicialmente, desenvolvemos esse sistema de forma a tornar o mais simples possível. Depois, devemos encontrar ∆ ,   N 1   e   N 2 para determinarmos os itens solicitados:

    Temos que cada um tem uma matriz, igual a:

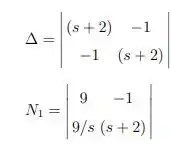
    Resolvendo essas matrizes, chegamos que:

    I 1 = N 1 ∆ = 9 s + 1 s ( s + 3 )

    I 2 = N 2 ∆ = 18 s ( s + 3 )

    Por fim:

    I a = I 1 = 3 s + 6 s + 3

    i b = 9 s - I 1 = 6 s - 6 s + 3

  2. Considerando as contas acima, temos:

    3. i a t = 3 1 + 2 e - 3 t u t A

    i b t = 6 1 - e - 3 t u t A

    Passo 2

  3. Considerando os itens acima, temos:

    4. V a = 10 s I b = 30 s 2 + 20 s - 20 s + 3

    V b = 10 s I 2 - I 1 = 30 s 2 - 40 s + 40 s + 3

    V c = 10 s 9 s - I 2 = 30 s 2 + 20 s - 20 s + 3

  4. Similarmente, temos:

    5. v a t = 30 t + 20 - 20 e - 3 t u t V

    v b t = 30 t - 40 + 40 e - 3 t u t V

    v c t = 30 t + 20 - 20 e - 3 t u t V

  5. Calculando o tempo quando a voltagem do capacitor atingir 1000 V, temos:

30 t + 20 - 20 e - 3 t = 1000

Ou seja:

30 t + 20 = 1000 → t = 32,67   s e g u n d o s

Resposta

  1. Item a:

    2. I a = 3 s + 6 s + 3

    i b = 6 s - 6 s + 3

  2. Item b:

    3. i a t = 3 1 + 2 e - 3 t u t A

    i b t = 6 1 - e - 3 t u t A

  3. Item c:

    4. V a = 30 s 2 + 20 s - 20 s + 3

    V b = 30 s 2 - 40 s + 40 s + 3

    V c = 30 s 2 + 20 s - 20 s + 3

  4. Item d:

    5. v a t = 30 t + 20 - 20 e - 3 t u t V

    v b t = 30 t - 40 + 40 e - 3 t u t V

    v c t = 30 t + 20 - 20 e - 3 t u t V

  5. Item e:

t = 32,67   s e g u n d o s

Exercícios de Livros Relacionados

Determine a tensão v o ( t ) no circuito da figura por meio da transformada de Laplace
Determine vo(t) no circuito da Figura 16.82 se vx(0) = 2 V e i(0) = 1 A.
Determine a transformada de Laplace da tensão mostrada na figura. Usando o valor de v s ( t ) no circuito mostrado na figura, determine o valor de v o ( t ) .
Considere o circuito RLC mostrado na figura e determine a resposta completa se v ( 0 ) = 2V quando a chave é fechada.
Determine i_0 ( t ) para t0 no circuito da figura.