Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 27

Não há nenhuma energia armazenada no circuito da Figura P13.27, no instante em que a fonte de corrente é ligada. Dado que i g = 100u(t) A:

a) Determine Io(s).

b) Use os teoremas dos valores inicial e final para determinar i 0 (0+) e i 0 ( ∞ ).

c) Os valores obtidos em (b) estão de acordo com o comportamento conhecido do circuito? Explique.

d) Determine i o (t).

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!

  1. Fazendo as devidas alterações de unidades pra trabalharmos melhor, temos:

    2. A partir disso, temos que:

    20 I ϕ + 25 I 0 - I ϕ + 25 ( I 0 - I 1 ) = 0

    Colocando I 1 em termos de I ϕ e simplificando ao máximo a equação, chegamos em:

    ( 5 s 2   +   6 s   +   10 ) I ϕ   +   - 5 s 2   -   5 s I o   =   600

    Sabendo que ∆   e   N 2 são iguais às seguintes matrizes:

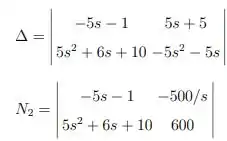
    Concluimos que:

    I 0 = N 2 ∆ = 20 s 2 - 96 s - 200 s ( s + 1 ) ( s + 2 )

    Passo 2

  2. Para t = 0 + , temos:

    3. i 0 0 + = lim ⁡ s I 0 = 20 A

    E para ∞ :

    i 0 ∞ = lim ⁡ s I 0 = - 200 2 = - 100   A

  3. Para t = 0 + , temos:

    4. Disso, tiramos que:

    I ϕ = I 0 0 + = 20 A → C O N F E R E !

    Para t = ∞ , temos:

    Disso, tiramos que:

    I 0 ∞ = - 10 0 A → C O N F E R E !

    Passo 3

  4. Temos que:

I 0 = 20 s 2 - 96 s - 200 s ( s + 1 ) ( s + 2 )

Decompondo em K, temos que: K 1 = - 100 ; K 2 = 84 ; K 3 = 36

Então temos:

I 0 = - 100 s + 84 s + 1 + 36 s + 2

Por fim:

i 0 t = - 100 + 84 e - t + 36 e - 2 t u t A

Resposta

  1. Item a:

    2. I 0 = 20 s 2 - 96 s - 200 s ( s + 1 ) ( s + 2 )

  2. Item b:

    3. i 0 0 + = lim ⁡ s I 0 = 20 A

    i 0 ∞ = lim ⁡ s I 0 = - 200 2 = - 100   A

  3. Item c: Sim.
  4. Item d:

i 0 t = - 100 + 84 e - t + 36 e - 2 t u t A

Exercícios de Livros Relacionados

A função na figura é movida da posição 1 para a 2 em t = 0 . Determine v ( t ) para todo t0 .
Considere o circuito RLC em paralelo da figura. Determine v ( t )ei ( t ) dado que v ( 0 ) = 5 e i ( 0 ) = 2A
Considere a Figura 16.81 e elabore um problema para ajudar outros estudantes a entender melhor a análise de circuitos no domínio s em circuitos com fontes dependentes.
Determine a resposta v R ( t ) para t0 no circuito da figura. Seja R = 3 Ω ,L = 2 HeC = 1 8 F .
Considere a figura e elabore um problema para ajudar outros estudantes a entenderem melhor o cálculo de tensões nodais no domínio s.