Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 9
A chave da figura 7.89 abre em . Determine para .
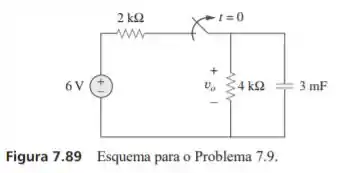
Passo 1
Da análise do circuito dado no exercício temos que para , a chave está fechada e assim podemos aplicar o divisor de tensão e obteremos
Agora, para temos um circuito sem fonte e nossa constante de tempo pode ser encontrada fazendo
Portanto, a nossa equação para será
Resposta
Exercícios de Livros Relacionados
a) Use os valores dos componentes do Apêndice H para criar um circuito RC de primeira ordem (veja a Figura 7.11) com uma constante de tempo de 50 ms. Use um único capacitor e uma rede de resistores, s
A chave no circuito visto na Figura P7.31 esteve na posição x por um longo tempo. Em t = 0, ela passa instantaneamente para a posição y. a) Determine a de modo que a constante de tempo para t . 0 seja
Na figura 8.1, assuma t 0 = 0 , V 0 = 1 0V , R = 1k Ω e C =1μ F . Calcule v , i e W c em t = 1 m s .Figura 8.1
Um circuito RC em série, consiste de um resistor de 2 0k Ω e um capacitor de 0,05μ F . Deseja-se descrever a corrente na rede por um fator de 5, sem mudança na tensão do capacitor. Calcule os valores
Em um circuito RC em série, determine:a) τ para R = 2k Ω e C =10μ F b) C para R = 10k Ω e τ =20μ s c) R para υ ( t ) no capacitor de 2μ F se reduzindo pela metade a cada 20 ms.