Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 54

A chave no circuito visto na Figura P7.54 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. Para t $ 0+, determine a) vo (t). b) i o (t).

Passo 1

[a] – Para t < 0 :

v 0 0 = 10000 15000 75 = 50   V

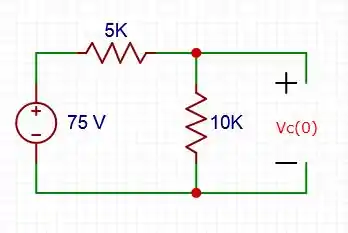
Para t ≥ 0 :

v 0 ∞ = 40000 50000 - 100 =   - 80   V

R e q = 40000 × 10000 40000 + 10000 = 8   k Ω

τ = R e q C = 8000 40 × 10 - 9 = 0,32   m s

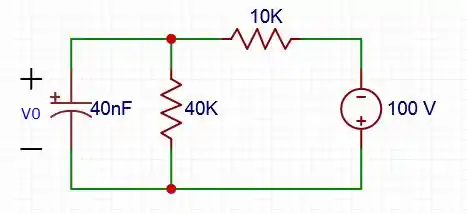
Partindo para a equação geral das tensões:

v 0 t = v 0 ∞ + v 0 0 - v 0 ∞ e - t τ  

Substituindo os valores, temos:

v 0 t =   - 80 + 50 + 80 e - 3125 t

v 0 t =   - 80 + 130 e - 3125 t   V

Passo 2

[b] – Para t ≥ 0 :

i 0 = 130 e - 3125 t - 80 + 100 10000 = 13 e - 3125 t + 2   m A

Resposta

a )   v 0 t =   - 80 + 130 e - 3125 t   V

b )   i 0 = 13 e - 3125 t + 2   m A

Exercícios de Livros Relacionados

Calcule v para t0 , se o circuito está em regime permanente em t = 0 - .
Calcule v para t0 , se o circuito está em regime permanente em t = 0 - .
Calcule v para t0, se v (0) = 2 V e (a) v_g = 4 V , (b) v_g = 6 e^(- t) V e (c) v_g = 6 e^(- 3 t) V .
Repita o Prob. 8.25, se a fonte de 36V e substituída por uma de 36 e - 3 t V com a mesma polaridade.
Considere um circuito sem fontes que tem uma resposta v t = v 0 e - t / τ V . Mostre que uma linha reta que é tangente ao gráfico desta resposta no tempo t 1 intercepta o eixo de tempo (abscissa) no t