Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 30

a) Use os valores dos componentes do Apêndice H para criar um circuito RC de primeira ordem (veja a Figura 7.11) com uma constante de tempo de 50 ms. Use um único capacitor e uma rede de resistores, se necessário. Desenhe seu circuito. b) Suponha que o capacitor que você escolheu em (a) tenha uma tensão inicial de 50 V. Escreva uma expressão para a queda de tensão no capacitor para t $ 0. c) Usando o resultado obtido em (b), calcule o tempo em que a queda de tensão no capacitor atinge 10 V.

Passo 1

[a] – Note que o problema tem muitas soluções corretas diferentes.

R = τ C

Escolhendo um capacitor de 100   μ F   do apêndice H, temos:

R = 0.05 100 × 10 - 6 = 500   Ω

Aqui, tem uma sacada, eu posso “construir” um resistor de 500   Ω pela combinação de dois resistores de 1   k Ω (No caso, em paralelo), logo, o circuito ficará da seguinte maneira.

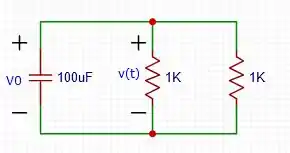
Passo 2

[b] – O problema já dá uma tensão inicial de 50   V , então:

v t = V 0 e - t / τ ,     t ≥ 0

Para a constante de tempo, temos:

τ = R C = 500 × 100 × 10 - 6 = 50   m s

Para sua inversa:

1 τ = 20

Logo,

v t = 50 e - 20 t   V ,     t ≥ 0

Passo 3

[c] – Para encontrar t , basta eliminar o e , e com isso calcular o l n .

50 e - 20 t = 10 → e 20 t   = 5

t = l n l n   5   20 = 80,47   m s

Resposta

a )   C i r c u i t o   d e m o n s t r a d o   n a   l e t r a   a

b )   v t = 50 e - 20 t   V ,     t ≥ 0

c )   t = l n l n   5   20 = 80,47   m s

Exercícios de Livros Relacionados

a) A chave no circuito da Figura P7.52 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b e permanece lá. Determine os valores inicial e final da tensão do c
A chave no circuito da Figura P7.53 esteve na posição a por um longo tempo. Em t = 0, ela é colocada na posição b. Calcule (a) a tensão inicial no capacitor; (b) a tensão final no capacitor; (c) a con
A chave no circuito visto na Figura P7.54 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. Para t $ 0+, determine a) vo (t). b) i o (t).
A chave do circuito visto na Figura P7.55 esteve na posição a por um longo tempo. Em t = 0, a chave passa instantaneamente para a posição b. Determine vo (t) e i o (t) para t $ 0+.
A chave do circuito na Figura P7.57 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. No instante em que a chave faz contato com o terminal b, a chave 2 ab