Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 49

A chave liga-antes-interrompe-depois do circuito da Figura P7.49 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. Determine a) vo (t), t $ 0+. b) i 1 (t), t $ 0. c) i 2 (t), t $ 0.

Passo 1

t < 0 : O circuito se configura da seguinte forma:

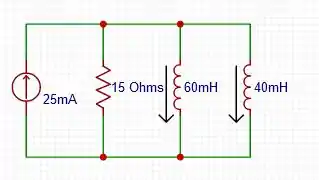
t > 0 : O circuito terá essa configuração:

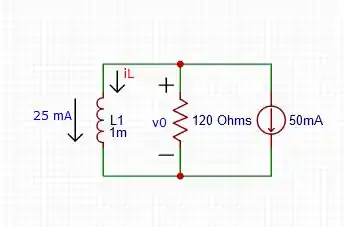
Como o indutor não pode variar a corrente instantaneamente, temos que:

i L 0 - = i L 0 + = 25   m A

Com isso, conseguimos calcular a constante de tempo:

τ = 24 × 10 - 3 120 = 0,2   m s → 1 τ = 5000

A corrente quando o circuito se estabiliza, é igual a:

i L ∞ =   - 50   m A  

Com isso, podemos calcular a corrente no indutor:

i L = - 50 + 25 + 50 e - 5000 t =   - 50 + 75 e - 5000 t   m A ,     t ≥ 0

E v 0

v 0 = - 120 75 × 10 - 3 e - 5000 t = - 9 e - 5000 t   V ,     t ≥ 0 +

Passo 2

[b] – A corrente no indutor 1 é usar a fórmula da corrente neste indutor:

i 1 = 1 60 × 10 - 3 ∫ 0 t - 9 e - 5000 x   d x + 10 × 10 - 3 ,     t ≥ 0

i 1 =   30 e - 5000 t - 20   m A ,     t ≥ 0

Passo 3

[c] – E aqui também 😊:

i 2 = 1 40 × 10 - 3 ∫ 0 t - 9 e - 5000 x   d x + 15 × 10 - 3

i 2 = 45 e - 5000 t - 30   m A ,     t ≥ 0

E terminamos a questão, até a próxima!

Resposta

a )   v 0 = - 9 e - 5000 t   V ,     t ≥ 0 +

b )   i 1 =   30 e - 5000 t - 20   m A ,     t ≥ 0

c )   i 2 = 45 e - 5000 t - 30   m A ,     t ≥ 0  

Exercícios de Livros Relacionados

A chave no circuito da Figura P7.47 esteve na posição 1 por um longo tempo. Em t = 0, ela passa instantaneamente para a posição 2. Em quantos milissegundos, depois do acionamento da chave, vo atinge 1
Suponha que a chave no circuito da Figura P7.51 esteve na posição a por um longo tempo e que em t = 0 ela é colocada na posição b. Determine (a) vC(0+); (b) vC(q); (c) t para t . 0; (d) i(0+); (e) vC,
A chave no circuito da Figura P7.14 esteve fechada por um longo tempo antes de abrir em t = 0. Determine vo (t) para t $ 0+.
A chave no circuito da Figura P7.15 esteve fechada por um longo tempo antes de abrir em t = 0. Determine a) i L(t), t $ 0. b) vL(t), t $ 0+. c) i Δ(t), t $ 0+.