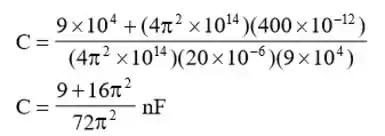Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas Abrangentes - Ex. 91
A Figura 9.91 mostra uma associação em paralelo entre uma indutância e uma resistência. Se for desejado conectar um capacitor em série com a associação em paralelo de modo que a impedância resultante seja resistiva em , qual será o valor necessário para ?
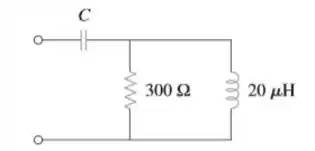
Passo 1
Então galera, pra essa questão que temos que calcular a capacitancia, aplicando atraves da freqeuencia. Portanto, vamos calcular a nossa impedancia do circuito!
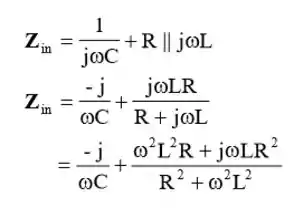
Passo 2
Para termos uma impedância puramente resistiva, a parte imaginaria tem que ser =0, portanto:
Onde,
Resposta
Exercícios de Livros Relacionados
Calcule a função de transferência de ganho de tensão para o quadripolo terminado em 1 Ω , mostrado na Fig. 14.16, com parâmetros z: Z 11 = 6 Ω , Z 12 = Z 21 = 4 Ω e Z 22 = 10 Ω .
Use os parâmetros ABCD para calcular V 2 / V 1 para o quadripolo terminado em um resistor de 1Ω se o quadripolo e a rede T da Fig. 14.13 com Z 1 = Z 2 = 2 s e Z 3 = 1 / s .
Calcule V 2 / V g , para o circuito mostrado abaixo.
Para o circuito R L C em serie com uma fonte de tensão v g , faça a função de rede ser H=I / V g , ondeI e a corrente fasorial. Mostre que as respostas em amplitude e fase são similares as da Fig. 15.
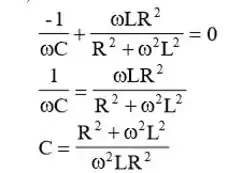
Faça R=4 Ω , L=1 / 10H e C=1 / 40F na Fig. 15.1 e calcule a amplitude máxima e o ponto onde ela ocorre. Esboce também as respostas em amplitude e fase.