Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 53
53- Determine no circuito da Figura
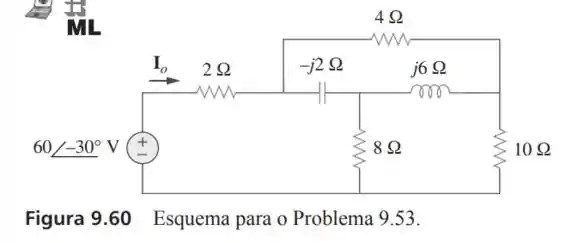
Passo 1
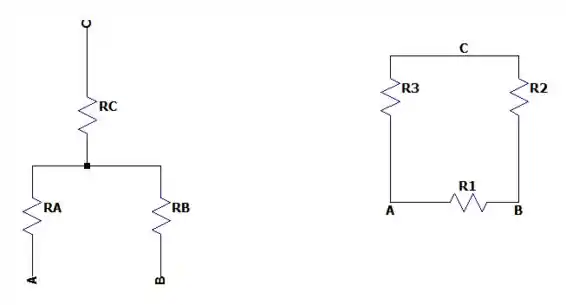
Um raciocínio para fazer essa questão é a de calcular a impedância equivalente do circuito, mas esse circuito é um circuito misto né? Fica um pouco chato de fazer por que temos que lembrar da conversão de triângulo para estrela e vice-versa. E nesse caso vamos fazer a transformação de estrela para triângulo das reatâncias e a resistência de fazendo a seguinte conta:
Deixando nosso circuito da seguinte forma:
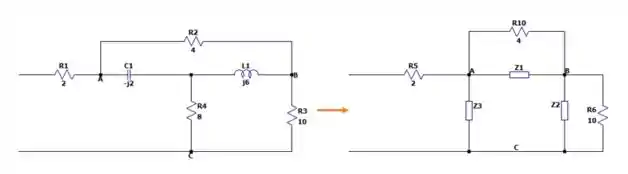
Não precisa nem dizer que tudo que é feito para essa transformação em corrente contínua é válida para corrente alternada.
Então:
Passo 2
Agora vamos começar a transformar o circuito a ponto de termos uma reatância apenas.
E para isso vamos fazer e .
E será:
Deixando o circuito com a seguinte cara:
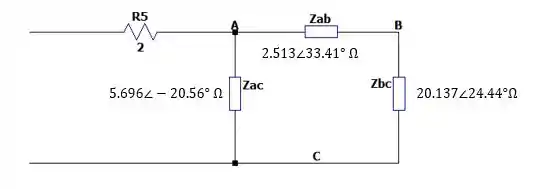
Passo 3
Aí a impedância equivalente do circuito é igual a:
O que seguindo a mesma lógica feita no passo anterior nós teremos:
Então a resistência equivalente será de:
Passo 4
O que nos dá finalmente uma corrente igual a:
Resposta
Alguns pequenos erros podem ser obtidos afinal convertemos de fasor para complexo diversas vezes.