Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 9.Problemas - Ex. 36

O fasor corrente Ib, no circuito da Figura P9.36, é 25 ∠   0 º mA..

a) Determine Ia, Ic e Ig.

b) Se v = 1.500 rad/s, determine as expressões para i a(t), i c (t) e i g(t).

Passo 1

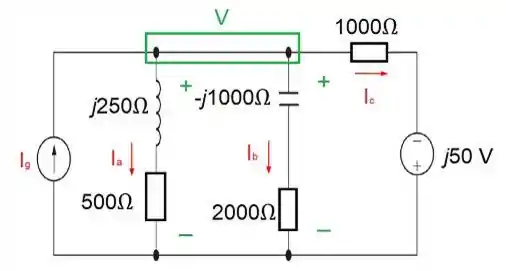
Beleza pessoal?! Espero que sim, para darmos início a resolução, primeiro você precisa prestar bastante atenção na figura acima, é dela que iremos extrair informações importantes para a resolução.

No nó marcado na figura, iremos considerar que a tensão é V.

Passo 2

  1. Aplicando a Lei de Ohm para determinar a voltagem V, temos;

    2. V = I b ∙ 2000 - j 1000

    V = 25 ∙ 10 - 3 ∙ 2000 - j 1000

    V   =   50 - j 25 =   55.9 ∠ - 26.57 º   V

    Sabemos então a voltagem através a impedância 500   +   j 250   Ω e nós podemos determinar então a corrente I a :

    I a   =   V 500   +   j 250

      =   55.9 ∠ - 26.57 º 559 ∠ 26.57 º

    =   100 ∠ - 53.14 º   m A

    Agora, utilizando a lei de Ohm iremos determinar a corrente I c :

    I c =   V   +   j 50 1000

    I c   =   0   -   j 25   +   j 50 1000

    I c   =   50   +   j 25 1000

    I c =   55.9 ∠ 26.57 º 1000

    I c   =   55.9 ∠ 26.57 º   m A

    Agora iremos finalmente encontrar I g

    I g   =   I a   +   I a   +   I c

      =   100 ∠ - 53.14 º   +   25 ∠ 0 º   + 55.9 ∠ 26.57 º  

      =   60   -   j 80   +   25   +   50   +   j 25

      =   135   -   j 55

    I g   =   145.8 ∠ - 2 2 . 1 7 º   m A  

    Passo 3

  2. Na letra a) nós determinamos os fasores das correntes. Agora nós podemos expressar a corrente em relação ao tempo. Para ω   =   1500   r d / s nós temos que:

i a t = 100 cos ⁡ 1500 t - 53.14 º m A

i b t = 55.9 cos ⁡ 1500 t + 26.57 º m A

i c t = 1 45.8 cos ⁡ 1500 t - 22 . 1 7 º m A

Resposta

Ver o desenvolvimento.

Exercícios de Livros Relacionados

Calcule a tensão v em regime permanente, usando análise nodal.
Calcule a tensão v em regime permanente, usando análise nodal.
Resolva o Ex. 11.1.2, usando análise de malha.
Calcule a corrente i em regime permanente.
Resolva o Ex. 11.1.1, usando análise de laço.