Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 46

Determine i_0 ( t ) no circuito da figura.

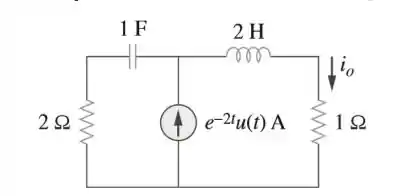
Passo 1

Vamos começar passando esse circuito para Laplace:

Passo 2

Agora, vamos apenas fazer uma análise nodal, simplesmente isso!

(1)/(s + 2) = (V ( s ))/(((1)/(s) + 2)) + (V ( s ))/(( 2 s + 1 ))

V ( s ) = (1)/(( s + 2 )) xx [((2 s + 1))/(( s + 1 ))]

V ( s ) = (( 2 s + 1 ))/(( s + 1 ) ( s + 2 ))

I_o ( s ) = (V ( s ))/(( 2 s + 1 ))

I_o ( s ) = (1)/(( 2 s + 1 )) xx (( 2 s + 1 ))/(( s + 1 ) ( s + 2 ))

I_o ( s ) = (1)/(( s + 1 ) ( s + 2 ))

I_o ( s ) = (1)/(s + 1) - (1)/(s + 2)

Passo 3

Daí, fazendo o Laplace inverso com nossas fórmulas de Laplace:

e^(- a t) f ( t ) harr F ( s + a )

Chegamos em:

i_o ( t ) = ( e^(- t) - e^(- 2 t) ) u ( t ) A

Resposta

i_o ( t ) = ( e^(- t) - e^(- 2 t) ) u ( t ) A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a figura e elabore um problema para ajudar outros estudantes a entenderem melhor o cálculo de tensões nodais no domínio s.
A função de transferência de certo circuito é H ( s ) = 5 s + 1 - 3 s + 2 + 6 s + 4 Determine a resposta ao impulso do circuito.
Quando a entrada de um sistema é uma função degrau unitário, a resposta é 10 c o s 2 u ( t ) . Obtenha a função de transferência do sistema.
Quando um degrau unitário é aplicado a um sistema em t = 0, sua resposta é y ( t ) = 4 + 1 2 e - 3 t - e - 2 t ( 2 c o s 4 t + 3 s e n 4 t ) u ( t ) .Qual a função de transferência desse sistema?
Considere o circuito da figura e determine H ( s ) = V o ( s ) V s ( s ) . Suponha condições iniciais zero.