Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 8.Problemas - Ex. 19
No circuito da Figura 8.1, R = 5 , L = 8 H, C = 125 nF, = 30 V e = 6 mA.
a) Determine para t 0.
b) Determine os primeiros três valores de t para os quais dv/dt é igual a zero. Esses valores devem ser denotados como
c) Mostre que .
d) Mostre que .
e) Calcule .
f) Faça um gráfico de para 0 t .
Passo 1
Faaaaala, pessoal!! Bora resolver mais uma questão juntos?
Para essa questãozinha aqui, no item (a), para determinarmos o valor de para t 0, devemos primeiro encontrar a resposta do circuito, a partir dos valores de , para então determinarmos a equação genérica de que melhor se aplica. Para isso, utilizaremos o seguinte:
Sendo assim, vemos que , portanto, utilizaremos a seguinte equação:
Passo 2
Continuando o item (a), encontraremos agora os valores de da seguinte maneira:
Para encontrarmos vamos igualar a 0:
Para encontrarmos , utilizaremos os valores de e :
Portanto, substituindo os valores na equação genérica, teremos:
Passo 3
Já partindo para o item (b), determinaremos os primeiros três valores de t para os quais dv/dt é igual a zero. Sendo assim, temos:
será zero quando , ou quando . Sendo assim:
Passo 4
Partindo para o item (c), sabemos que . Além disso, sabemos que , portanto:
Desse modo, provamos que:
Passo 5
Partindo para o item (c), sabemos que . Além disso, sabemos que , portanto:
Desse modo, provamos que:
Passo 6
No item (d), basta substituirmos os valores de encontrados no passo 3, na fórmula do passo 2. Sendo assim, teremos:
Passo 7
Por fim, plotando o gráfico de para 0 t , temos que:
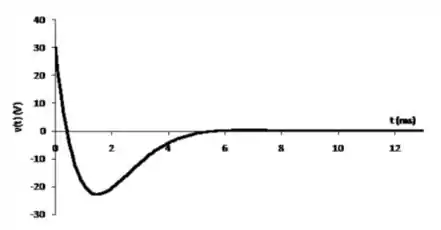
Prontinho, pessoal!! Bora resolver mais uma questão juntos?
Resposta
a) .
b) ; ; .
c) Resolução nos passos acima.
d) Resolução nos passos acima.
e); ;
f)
