Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 10.Problemas - Ex. 60

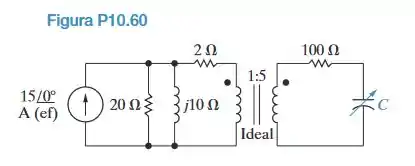
A fonte de tensão senoidal no circuito da Figura P10.60 está operando em uma frequência de 20 krad/s. A reatância capacitiva variável do circuito é ajustada até que a potência média fornecida ao resistor de 100 V seja a maior possível.

a) Determine o valor de C em microfarads.

b) Quando C tiver o valor determinado em (a), qual será a potência média fornecida ao resistor de 100 V?

c) Substitua o resistor de 100 V por um resistor variável R o . Especifique o valor de R o de modo que lhe seja fornecida máxima potência média.

d) Qual é a máxima potência média que pode ser fornecida a R o ?

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

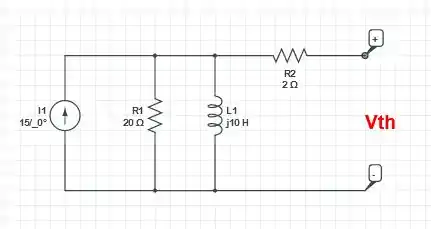
A – Primeiramente, vamos desconectar o enrolamento primário conforme mostrado no circuito, logo após, vamos determinar o equivalente de Thevenin V t h através nos terminais do enrolamento primário

V t h = 15 ∠ 0 ° 20   j 10

Logo, nós temos que

V t h = 15 20 j 10 20 + j 10 = 60 + j 120   V ( r m s )

Desativando a fonte de corrente e determinando a impedância equivalente de Thevenin Z t h , nós temos que

Z t h = 2 + 20     j 10

Com isso,

Z t h = 2 + ( 20 ) ( j 10 ) 20 + j 10 = 6 + j 8   Ω

A potência média máxima é transferida para o resistor de 100   Ω se a impedância Z p vista através do enrolamento primário em relação ao lado secundário for compatível com Z t h

Z p = Z t h *   ( 1 )

E a análise será feita a partir desse circuito

Passo 2

Como o transformador é ideal, o valor de Z p é dado por

Z p = 1 25 ( 100 - j X C )

Fazendo a substituição,

Z p = 4 - j X C 25   Ω

Desde que R e Z p ≠ R e { Z t h } , a potência média máxima é transferida para o resistor de 100   Ω se I m Z p = - I m { Z t h } . Determinando a reatância X C que a potência máxima será transferida para o resistor de 100   Ω

I m Z p = - I m Z t h

Com isso, nós temos que

X C 25 = 8

Portanto,

X C = 200   Ω

Agora nós já podemos determinar o valor de C que permite que o máximo de potência média seja transferido para o resistor de 100   Ω

C = 1 ω X c

Fazendo a substituição,

C = 1 ( 20 × 10 3 ) ( 200 ) = 0,25   μ F

Logo,

C = 0,25   μ F

Passo 3

B - Conectando a impedância calculada Z p ao circuito equivalente de Thevenin, e com isso, conseguindo obter a corrente I fluindo através da impedância Z p

I = V t h R t h + R p

Fazendo a substituição,

I = 60 + j 120 10 = 6 + j 12

Passando para fasores, nós temos que

I = 13,42 ∠ 63,43 °   A ( r m s )

A potência média P transferida para a impedância Z p

P = I 2 R p

Substituindo os valores, nós temos que

P = 13,42 2 4 = 720   W

Onde

R p = R e { Z p }

Passo 4

C – A impedância Z p é dada por

Z p = 1 25 R o - j 200 = R o 25 - j 8   Ω

De (1), vamos determinar o valor de R o para que o máximo de potência média seja transferido

Z p = Z t h *

Fazendo as devidas substituições,

R o 25 - j 8 = 6 - j 8

Portanto,

R o = 150   Ω

Passo 5

D – A impedância Z p é agora dada por

Z p = 6 - j 8   Ω

Conectando a impedância calculada Z p para o circuito equivalente de Thevenin, e com isso, calculando a corrente I através da impedância Z p

I = V t h R t h + R p

Substituindo os valores,

I = 60 + j 120 12 = 5 + j 10

Em fasores, nós temos que

I = 11,18 ∠ 63,43 °   A ( r m s )

Determinando a potência média P transferida para a impedância Z p

P = I 2 R p

Fazendo a substituição

P = 11,18 2 6 = 750   W

Resposta

a )   C = 0,25   μ F

b )   P = 720   W

c )   R o = 150   Ω

d )   P = 750   W

Exercícios de Livros Relacionados

Prove que, se apenas o módulo da impedância de uma carga puder variar, a maior potência média lhe será transferida quando Z L = | Z t h | . [Sugestão: ao deduzir a expressão para a potência média da c
a) Determine a potência média dissipada em cada resistor no circuito da Figura P10.39.b) Confirme sua resposta demonstrando que a potência total fornecida é igual à potência total absorvida.
O fasor tensão V a b , no circuito da Figura P10.43, é 300 ∠ 0 °V ( e f ) , quando nenhuma carga externa está ligada aos terminais a, b. Quando uma carga de impedância 200 - j 500Ω é ligada aos termin
a) Determine a potência média dissipada na linha na Figura P10.31.b) Determine a reatância capacitiva que, quando ligada em paralelo com a carga, fará com que esta se comporte como uma carga puramente
O resistor variável no circuito da Figura P10.46 é ajustado até que a potência média que ele absorve seja máxima.a) Determine R.b) Determine a máxima potência média.c) Encontre um resistor no Apêndice