Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 52
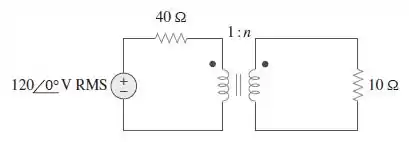
Para o circuito da Figura , determine a relação de espiras que resultará na transferência de máxima potência média para a carga. Calcule a máxima potência média.
Passo 1
Considere o circuito abaixo. A impedância da carga pode ser refletida no lado primário do transformador. Desse modo,
Para termos a máxima transferência de energia, precisamos considerar o equivalente de Thevenin. Assim, seja e . Logo,
Passo 2
Aqui estamos trabalhando com um transformador ideal, ou seja, não temos perda. Assim, a potência fornecida ao primário é igual ao secundário:
Resposta
A relação de espiras é igual a:
A máxima potência média é igual a:
Exercícios de Livros Relacionados
Um receptor de rádio tem resistência de 300Ω . Quando conectado diretamente a uma antena com impedância característica de 75Ω ocorre um descasamento de impedância. Inserindo-se um transformador casado
Um circuito de amplificador estéreo com impedância de saída de 7,2 k Ω deve ser casado com um alto-falante com impedância de entrada de 8Ω por um transformador cujo primário possui 3.000 espiras. Calc
O sistema trifásico de uma torre distribui energia elétrica com uma tensão de linha de 13.2 k V . Um transformador em um poste conectado a um único fio e a terra abaixa a alta tensão para 120 V r m s
Um transformador de 4 k V A , 2.400 / 240 V tem 250e s p i r a s no primário. Calcule:a) A relação de espirasb) O número de espiras no secundárioc) As correntes no primário e no secundário
Um transformador de distribuição de 25.000 / 240V r m s tem uma corrente primária de valor nominal 75 A .a)Determine o valor nominal em k V A para esse transformadorb)Calcule a corrente no secundário.