Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 57

Para o transformador ideal da Figura 13.122 a seguir, determine:

  1. I 1 e I 2
  2. V 1 ,   V 2 e V 0
  3. A potência complexa fornecida pela fonte

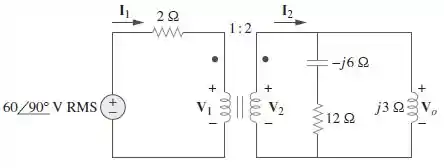
Passo 1

Galera, vamos pra letra (a). A carga ligada Z L ao transformador é dada por:

Z L = 12 - j 6   | |   j 3

Z L = 12 - j 6 j 3 12 - j 6 + j 3

Z L = 0,706 + j 3,176   Ω

A impedância da carga pode ser refletia para o primário! Assim,

Z R = Z L n 2

Z R = 0,706 + j 3,176 2 2

Z R = 0,706 + j 3,176 4

Z R = 0,176 + j 0,794   Ω

Com essa informação na mão, podemos facilmente calcular a corrente no primário do transformador:

I 1 = V 2 + Z R

I 1 = 60 ∠ 90 ° 1 + 0,176 + j 0,794 = 25,9 ∠ 69,95 °   A

A corrente do secundário é:

I 1 I 2 = 2 1

I 2 = 15,9 ∠ 69,95 ° 2

I 2 = 12,95 ∠ 69,95 °   A

Passo 2

Vamos para a letra (b) agora. Dá uma olhada pro lado primário do transformador. Para encontrarmos V 1 , podemos usar o divisor de tensão!

V 1 = 60 ∠ 90 ° Z R Z R + 2

V 1 = 60 ∠ 90 ° 0,176 + j 0,794 0,177 + j 0,794 + 2

V 1 = 21,07 ∠ 147,46 °   V

Nos terminais do transformador:

V 1 V 2 = 1 2

V 2 = 2 V 1 = 42,14 ∠ 147,46 °   V

Como a tensão V 0 está no componente em paralelo aos enrolamentos do trafo,

V 0 = V 2 = 42,14 ∠ 147,46 °   V

Passo 3

A potência complexa fornecia pela fonte de tensão pode ser calculada por:

S = 60 ∠ 90 ° I 1 *

S = 60 ∠ 90 ° 25,9 ∠ - 69,95 °

S = 1554 ∠ 20,05 °   V A

Resposta

  1. I 1 = 25,9 ∠ 69,95 °   A e I 2 = 12,95 ∠ 69,95 °   A
  2. V 1 = 21,07 ∠ 147,46 °   V , V 2 = 42,14 ∠ 147,46 °   V e V 0 = 42,14 ∠ 147,46 °   V
  3. S = 1554 ∠ 20,05 °   V A
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

38. Um transformador de 4,6k V A , 2300 / 115V , 60H z foi projetado para ter uma f . e . m induzida de 2,5V o l t s / e s p i r a . Supondo o transformador ideal, calcule:a) O número de espiras do en
40. O primário de um transformador ideal com relação de espiras igual a 5 é conectado a uma fonte de tensão com parâmetros de T h é v e n i n é V T h = 10c o s2.000 tV e R T h = 100Ω . Determine a pot
42. Considere o circuito da figura 13.107 e determine a potência absorvida pelo resistor de 2Ω . Suponha que 80V seja um valor R M S .
41. Determine I 1 e I 2 no circuito abaixo.
43. Obtenha V 1 e V 2 no circuito do transformador ideal da Figura 13.108.